Geometry 7.1 Pythagorean Theorem Lesson
... Use the Pythagorean Theorem to find the lengths of the missing sides of a triangle - SIMPLIFY any square roots! ...
... Use the Pythagorean Theorem to find the lengths of the missing sides of a triangle - SIMPLIFY any square roots! ...
Molecular Geometry
... • Use the Lewis Structure to determine the geometry of the molecule. • Focus only on the CENTRAL atom for all molecules! Count the number of electron regions. • Look for REGIONS WHERE ELECTRONS ARE FOUND rather than number of bonds. (Ex: Double and Triple bonds count as 1 region) ...
... • Use the Lewis Structure to determine the geometry of the molecule. • Focus only on the CENTRAL atom for all molecules! Count the number of electron regions. • Look for REGIONS WHERE ELECTRONS ARE FOUND rather than number of bonds. (Ex: Double and Triple bonds count as 1 region) ...
Introduction to the Axiomatic Method
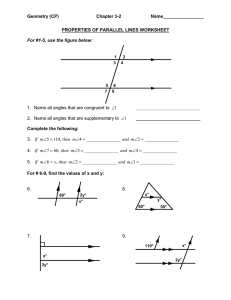
... that there are at least two lines through P parallel to L. ...
... that there are at least two lines through P parallel to L. ...
Chapter 1
... Euclid says, “To extend a finite straight line continuously in a straight line.” In modern times it is often paraphrased as, “A straight line can be extended indefinitely in either direction,” and the parallel postulate does not make much sense without this understanding. Presumably Greenberg has st ...
... Euclid says, “To extend a finite straight line continuously in a straight line.” In modern times it is often paraphrased as, “A straight line can be extended indefinitely in either direction,” and the parallel postulate does not make much sense without this understanding. Presumably Greenberg has st ...
3/6 Quiz Review with reference sheet and answers File
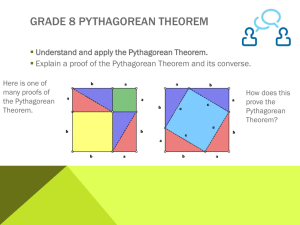
... The length of each side of a triangle must be less than the sum of the lengths of the other two sides. Tips for classifying quadrilaterals: First check if it’s a parallelogram (both pairs opp. sides ≅, diagonals bisect each other, etc.). Then use converse of Pythagorean theorem to check for right an ...
... The length of each side of a triangle must be less than the sum of the lengths of the other two sides. Tips for classifying quadrilaterals: First check if it’s a parallelogram (both pairs opp. sides ≅, diagonals bisect each other, etc.). Then use converse of Pythagorean theorem to check for right an ...
Seminar Geometry
... analyze geometric figures using deductive reasoning, make conjectures and formulate hypotheses, draw conclusions and make connections with other mathematical concepts, and model situations geometrically as a problem solving strategy. Algebraic and geometric skills are integrated throughout the curri ...
... analyze geometric figures using deductive reasoning, make conjectures and formulate hypotheses, draw conclusions and make connections with other mathematical concepts, and model situations geometrically as a problem solving strategy. Algebraic and geometric skills are integrated throughout the curri ...
PDF
... The following theorem holds in any geometry in which SAS is valid. Specifically, it holds in both Euclidean geometry and hyperbolic geometry (and therefore in neutral geometry) as well as in spherical geometry. Theorem 1. The angles opposite to the congruent sides of an isosceles triangle are congru ...
... The following theorem holds in any geometry in which SAS is valid. Specifically, it holds in both Euclidean geometry and hyperbolic geometry (and therefore in neutral geometry) as well as in spherical geometry. Theorem 1. The angles opposite to the congruent sides of an isosceles triangle are congru ...
Read the history below and answer the questions that follow
... one of the three greatest mathematicians of all time, invented non-Euclidian geometry prior to the independent work of Janos Bolyai (1802–1860) and Nikolai Lobachevsky (1792-1856). NonEuclidian geometry generally refers to any geometry not based on the postulates of Euclid, including geometries for ...
... one of the three greatest mathematicians of all time, invented non-Euclidian geometry prior to the independent work of Janos Bolyai (1802–1860) and Nikolai Lobachevsky (1792-1856). NonEuclidian geometry generally refers to any geometry not based on the postulates of Euclid, including geometries for ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)