Rectangles - BakerMath.org
... bisect each other and they are congruent. How does he know that the corners are angles? ...
... bisect each other and they are congruent. How does he know that the corners are angles? ...
Lesson 2 - Inequalities and Triangles
... a. all angles whose measures are less than m2 By Exterior Angle Inequality Theorem, m2 > m4 and m2 > m1, m2 > m1 + m7, and m2 > m3. Thus, the measures of 1, 3, 4, and 7 are all less than m2 . b. all angles whose measures are greater than m3 By Exterior Angle Inequality Theorem, m4 > ...
... a. all angles whose measures are less than m2 By Exterior Angle Inequality Theorem, m2 > m4 and m2 > m1, m2 > m1 + m7, and m2 > m3. Thus, the measures of 1, 3, 4, and 7 are all less than m2 . b. all angles whose measures are greater than m3 By Exterior Angle Inequality Theorem, m4 > ...
Pre-AP Geometry
... G-CO.4 Develop definitions of rotations, reflections, and translation in terms of angles, circles, perpendicular lines, parallel lines, and line segments. G-CO.5 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, ...
... G-CO.4 Develop definitions of rotations, reflections, and translation in terms of angles, circles, perpendicular lines, parallel lines, and line segments. G-CO.5 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, ...
Geometry 1 - Skyline Prep High School
... Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. For example, rearrange Ohm’s law V = IR to highlight resistance R. Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, startin ...
... Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. For example, rearrange Ohm’s law V = IR to highlight resistance R. Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, startin ...
Name - North Penn School District
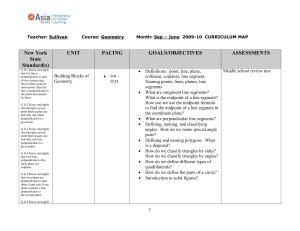
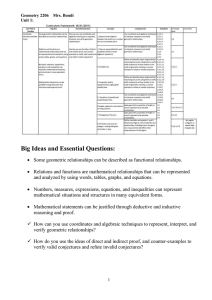
... Big Ideas and Essential Questions: Some geometric relationships can be described as functional relationships. Relations and functions are mathematical relationships that can be represented and analyzed by using words, tables, graphs, and equations. Numbers, measures, expressions, equations, an ...
... Big Ideas and Essential Questions: Some geometric relationships can be described as functional relationships. Relations and functions are mathematical relationships that can be represented and analyzed by using words, tables, graphs, and equations. Numbers, measures, expressions, equations, an ...
(Points, Lines, Planes and Transformations)
... Lines in the same plane that are always the same distance apart. They do not intersect. Skew lines Lines that are not in the same plane and do not intersect. Intersection The set of points that are in both figures. Concurrent lines Three or more lines that pass through the same point. Post ...
... Lines in the same plane that are always the same distance apart. They do not intersect. Skew lines Lines that are not in the same plane and do not intersect. Intersection The set of points that are in both figures. Concurrent lines Three or more lines that pass through the same point. Post ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)