Lesson 4-1
... Answer: ΔJMN has no congruent sides, so it is a scalene triangle. ΔJKO has no congruent sides, so it is a scalene triangle. ΔOLN has all sides congruent, so it is an equilateral triangle. ...
... Answer: ΔJMN has no congruent sides, so it is a scalene triangle. ΔJKO has no congruent sides, so it is a scalene triangle. ΔOLN has all sides congruent, so it is an equilateral triangle. ...
Section 2.4 Notes: Congruent Supplements and Complements
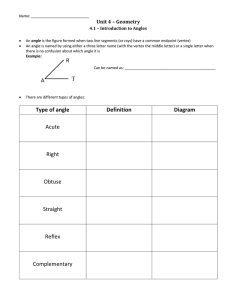
... Name: ____________________________________________ ...
... Name: ____________________________________________ ...
Ch 5
... Theorem 5.23 – The diagonals of a rhombus are perpendicular to each other. A If D B then C Theorem 5.24 – If the diagonals of a parallelogram are perpendicular to each other, then the parallelogram is a rhombus. Since this is the converse of theorem 5.23 write the biconditional statement. ...
... Theorem 5.23 – The diagonals of a rhombus are perpendicular to each other. A If D B then C Theorem 5.24 – If the diagonals of a parallelogram are perpendicular to each other, then the parallelogram is a rhombus. Since this is the converse of theorem 5.23 write the biconditional statement. ...
Full text
... Pascal triangle where rising diagonals sum to give the Fibonacci numbers 1, 1, 2, 3, 5, 8, ... . The seventh diagonal in our array is 15 7, 14, 7; the eleventh diagonal is 1, 11, 44, 77, 55, 11. This suggests the following. Theorem 1. The number D ) 2 is a prime number if and only if every entry tha ...
... Pascal triangle where rising diagonals sum to give the Fibonacci numbers 1, 1, 2, 3, 5, 8, ... . The seventh diagonal in our array is 15 7, 14, 7; the eleventh diagonal is 1, 11, 44, 77, 55, 11. This suggests the following. Theorem 1. The number D ) 2 is a prime number if and only if every entry tha ...