Complementary and Supplementary Angles
... angles are two angles whose sum is 180° (or a straight angle). Each of the two angles is called the supplement of the other ...
... angles are two angles whose sum is 180° (or a straight angle). Each of the two angles is called the supplement of the other ...
geometry
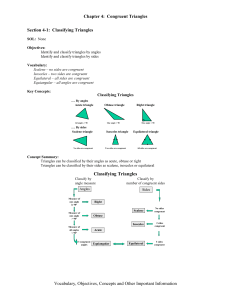
... MISCONCEPTIONS (What are the typical errors or difficult areas? Also suggest ways to teach them.) • Students tend to forget that angle and segment correspondence is critical for determining if the triangles are congruent. o Have students determine which two parts are given (either two angles or two ...
... MISCONCEPTIONS (What are the typical errors or difficult areas? Also suggest ways to teach them.) • Students tend to forget that angle and segment correspondence is critical for determining if the triangles are congruent. o Have students determine which two parts are given (either two angles or two ...
Chapter 4 Notes - Stevenson High School
... geometric figures. I can apply the concepts of congruence to solve problems. I can prove relationships in geometric figures (i.e. prove triangles and corresponding parts are congruent). I can determine and justify when two triangles are congruent (including ASA, SAS, AAS, HL and SSS Theorems). ...
... geometric figures. I can apply the concepts of congruence to solve problems. I can prove relationships in geometric figures (i.e. prove triangles and corresponding parts are congruent). I can determine and justify when two triangles are congruent (including ASA, SAS, AAS, HL and SSS Theorems). ...
Discovery of Non-Euclidean Geometry
... (a) Let Σ1 be the set of points Y ∈ r(Q, R) such that the ray r(P, Y ) does not meet l, and Σ2 the complement of Σ1 in QR. It is easy to see that both Σ1 , Σ2 are convex. So Σ1 , Σ2 form a Dedekind cut of QR. Then there exists a unique point X ∈ QR such that Σ1 , Σ2 are two rays (one of them is an o ...
... (a) Let Σ1 be the set of points Y ∈ r(Q, R) such that the ray r(P, Y ) does not meet l, and Σ2 the complement of Σ1 in QR. It is easy to see that both Σ1 , Σ2 are convex. So Σ1 , Σ2 form a Dedekind cut of QR. Then there exists a unique point X ∈ QR such that Σ1 , Σ2 are two rays (one of them is an o ...
Interior and Exterior Angles of Triangles
... **The students must complete the Interior Angles Activity first!** Ask if there are any questions before they begin. ...
... **The students must complete the Interior Angles Activity first!** Ask if there are any questions before they begin. ...