Interactive Chalkboard - Tuslaw Local School District
... The vertices of ABC are A(–3, 7), B(–1, 0), and C(5, 5). Graph the triangle and the image of ABC after a translation 4 units right and 5 units down. This translation can be written as the ordered pair (4, –5). To find the coordinates of the translated image, add 4 to each x-coordinate and add –5 ...
... The vertices of ABC are A(–3, 7), B(–1, 0), and C(5, 5). Graph the triangle and the image of ABC after a translation 4 units right and 5 units down. This translation can be written as the ordered pair (4, –5). To find the coordinates of the translated image, add 4 to each x-coordinate and add –5 ...
Chapter 2 Resource Masters
... 9. Properties of Equality, postulates, and theorems can all be used to justify steps in a proof. 10. Once a statement has been proved, it can be used to prove other statements. 11. If two angles form a linear pair, then they are complimentary angles. 12. Congruence of angles is reflexive and symmetr ...
... 9. Properties of Equality, postulates, and theorems can all be used to justify steps in a proof. 10. Once a statement has been proved, it can be used to prove other statements. 11. If two angles form a linear pair, then they are complimentary angles. 12. Congruence of angles is reflexive and symmetr ...
tetrahedron - PlanetMath.org
... in three pairs such that the edges of a pair do not intersect. A tetrahedron is always convex. In many ways, the geometry of a tetrahedron is the three-dimensional analogue of the geometry of the triangle in two dimensions. In particular, the special points associated to a triangle have their three- ...
... in three pairs such that the edges of a pair do not intersect. A tetrahedron is always convex. In many ways, the geometry of a tetrahedron is the three-dimensional analogue of the geometry of the triangle in two dimensions. In particular, the special points associated to a triangle have their three- ...
document
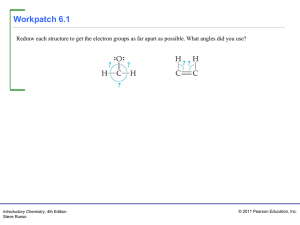
... For each molecule or polyatomic ion in the following five problems, (a) draw the electron-group geometry, (b) name the shape of the molecule, and (c) estimate the size of all the bond angles in the molecule or ion. (Some of the molecules and ions have lone pairs on the central atom.) ...
... For each molecule or polyatomic ion in the following five problems, (a) draw the electron-group geometry, (b) name the shape of the molecule, and (c) estimate the size of all the bond angles in the molecule or ion. (Some of the molecules and ions have lone pairs on the central atom.) ...
Lessons in this Unit
... Solve problems involving measurement and conversion of measurements from a larger unit to a smaller unit. 4.MD.3. Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the len ...
... Solve problems involving measurement and conversion of measurements from a larger unit to a smaller unit. 4.MD.3. Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the len ...
Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.For more than two thousand years, the adjective ""Euclidean"" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only where the gravitational field is weak.Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms to propositions without the use of coordinates. This is in contrast to analytic geometry, which uses coordinates.