Bessel Functions and Their Application to the Eigenvalues of the
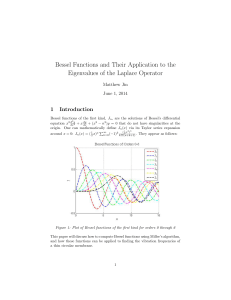
... The first task in this project was to compute Bessel functions, which was done using Miller’s downwards recurrence algorithm. The algorithm applies the recurrence relation Jn−1 (x) = 2n x Jn (x) − Jn+1 (x), where n is the order of Bessel function J—it computes Bessel functions in descending order fr ...
... The first task in this project was to compute Bessel functions, which was done using Miller’s downwards recurrence algorithm. The algorithm applies the recurrence relation Jn−1 (x) = 2n x Jn (x) − Jn+1 (x), where n is the order of Bessel function J—it computes Bessel functions in descending order fr ...
Unsupervised Feature Selection for the k
... a priori guarantees regarding the quality of the clustering after feature selection is performed, we chose to report results on the optimal value of the k-means clustering objective (the Fopt of Definition 1). This metric of accuracy has been extensively used in the Theoretical Computer Science comm ...
... a priori guarantees regarding the quality of the clustering after feature selection is performed, we chose to report results on the optimal value of the k-means clustering objective (the Fopt of Definition 1). This metric of accuracy has been extensively used in the Theoretical Computer Science comm ...
A+B
... Big-Omega and Big-Theta Nation • Definition 2: Let f and g be functions from the set of integers or the set of real numbers to the set of real numbers. • We say that f(x) is Ω(g(x)) if there are positive constants C and k such that |f(x)|≥ C|g(x)| Whenever x > k. ( this is read as “f(x) is big-Omeg ...
... Big-Omega and Big-Theta Nation • Definition 2: Let f and g be functions from the set of integers or the set of real numbers to the set of real numbers. • We say that f(x) is Ω(g(x)) if there are positive constants C and k such that |f(x)|≥ C|g(x)| Whenever x > k. ( this is read as “f(x) is big-Omeg ...
Introduction to Computer Science
... Information stored and processed by computer is a small fragment of reality containing essential data to solve stated problem. We have to think which informations are essential, which can help us and which are completely useless. We have to think how we will represent choosen informations. The last ...
... Information stored and processed by computer is a small fragment of reality containing essential data to solve stated problem. We have to think which informations are essential, which can help us and which are completely useless. We have to think how we will represent choosen informations. The last ...
Developing And Comparing Numerical Methods For Computing The Inverse Fourier Transform Abstract
... The Fourier transform is (up to a negative sign and a scalar factor depending on the definition used) its own inverse. Thus, a numerical method that computes one, computes the other. However, with the exception of the Gaussian function ( e x ), functions and their Fourier transforms have different ...
... The Fourier transform is (up to a negative sign and a scalar factor depending on the definition used) its own inverse. Thus, a numerical method that computes one, computes the other. However, with the exception of the Gaussian function ( e x ), functions and their Fourier transforms have different ...
6.896 Project Presentations
... Design and implement a dynamic processorallocation system for adaptively parallel jobs (jobs for which the number of processors that can be used without waste varies during execution) The problem of allocating processors to adaptively parallel jobs is called the adaptively parallel processor-allocat ...
... Design and implement a dynamic processorallocation system for adaptively parallel jobs (jobs for which the number of processors that can be used without waste varies during execution) The problem of allocating processors to adaptively parallel jobs is called the adaptively parallel processor-allocat ...