VMHS Math Circle
... primes (3, 5, 7, …). If you notice that you don’t have integer quotients, after dividing by a lot of primes, and that those quotients are less than the prime you’ve divided by, you probably have a prime number. Does this sound a bit confusing? Let’s try an example. Is the number 499 prime? If not, w ...
... primes (3, 5, 7, …). If you notice that you don’t have integer quotients, after dividing by a lot of primes, and that those quotients are less than the prime you’ve divided by, you probably have a prime number. Does this sound a bit confusing? Let’s try an example. Is the number 499 prime? If not, w ...
1811 Solution to POJ1811
... Complexity: O(N3/4/logN) for time, O(N1/2/logN) for space Estimation of time consumption: Finding all 7,603,553 primes smaller than 227 takes approx. 1.32 x 1011 divisions or 73 minutes on a Pentium 1.5 GHz. ...
... Complexity: O(N3/4/logN) for time, O(N1/2/logN) for space Estimation of time consumption: Finding all 7,603,553 primes smaller than 227 takes approx. 1.32 x 1011 divisions or 73 minutes on a Pentium 1.5 GHz. ...
Not Every Number is the Sum or Difference of Two Prime Powers
... M - 2" has all its prime factors greater than 330. On the other hand, by using more primes we can dispense with 3; that is, we can find an M and a set of 42 primes so that ...
... M - 2" has all its prime factors greater than 330. On the other hand, by using more primes we can dispense with 3; that is, we can find an M and a set of 42 primes so that ...
Slide 1
... Numbers To write 330 using its prime factorization, start breaking it up into smaller factors until there are no more composite numbers. 330=33x10=3x11x2x5 ...
... Numbers To write 330 using its prime factorization, start breaking it up into smaller factors until there are no more composite numbers. 330=33x10=3x11x2x5 ...
Greatest Common Factor
... • So, they are numbers that have more multiples than just one and itself. • For example, the factors of 28 are: • 1 x 28 • 2 x 14 • 4x7 ...
... • So, they are numbers that have more multiples than just one and itself. • For example, the factors of 28 are: • 1 x 28 • 2 x 14 • 4x7 ...
proof of Wilson`s theorem using the Wilson quotient
... Therefore, (n − 1)! being the product of the numbers from 1 to n − 1 includes among its divisors the greatest prime factor of n, and indeed all its divisors. Since two consecutive integers are always coprime, it is the case that gcd((n − 1)!, (n − 1)! + 1) = 1. Therefore n will divide (n − 1)! evenl ...
... Therefore, (n − 1)! being the product of the numbers from 1 to n − 1 includes among its divisors the greatest prime factor of n, and indeed all its divisors. Since two consecutive integers are always coprime, it is the case that gcd((n − 1)!, (n − 1)! + 1) = 1. Therefore n will divide (n − 1)! evenl ...
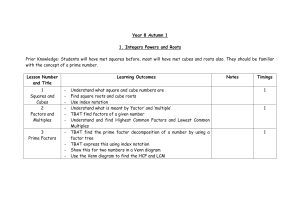
Integers Powers and Roots MTP
... Prior Knowledge: Students will have met squares before, most will have met cubes and roots also. They should be familiar with the concept of a prime number. Lesson Number and Title ...
... Prior Knowledge: Students will have met squares before, most will have met cubes and roots also. They should be familiar with the concept of a prime number. Lesson Number and Title ...
Sieve of Eratosthenes

In mathematics, the sieve of Eratosthenes (Ancient Greek: κόσκινον Ἐρατοσθένους, kóskinon Eratosthénous), one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the multiples of 2.The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime. This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime.The sieve of Eratosthenes is one of the most efficient ways to find all of the smaller primes. It is named after Eratosthenes of Cyrene, a Greek mathematician; although none of his works have survived, the sieve was described and attributed to Eratosthenes in the Introduction to Arithmetic by Nicomachus.The sieve may be used to find primes in arithmetic progressions.