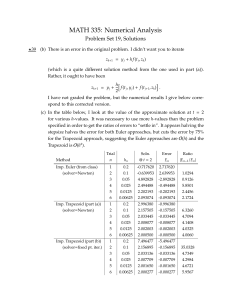
Optimal Stopping and Free-Boundary Problems Series
... horizon is also dynamic programming derived. The (the Bellman’s principle). same problems The method of are studied, essential supremum replacing the solves the problem in the Wiener processes case of infinite horizon N by Poisson random ...
... horizon is also dynamic programming derived. The (the Bellman’s principle). same problems The method of are studied, essential supremum replacing the solves the problem in the Wiener processes case of infinite horizon N by Poisson random ...
LINEAR PROGRAMMING MODELS
... z = 3 x1 + 5 x2 Moving along x2 would make z larger. − Optimality Test: z = 30. It is better than Ai but is it the best? − Iteration: Move to C. Why? There is no point else but C to move. − Optimality Test: z = 36. It is better than B, but is it the best? − Iteration: move to D. Why? − Optimality Te ...
... z = 3 x1 + 5 x2 Moving along x2 would make z larger. − Optimality Test: z = 30. It is better than Ai but is it the best? − Iteration: Move to C. Why? There is no point else but C to move. − Optimality Test: z = 36. It is better than B, but is it the best? − Iteration: move to D. Why? − Optimality Te ...
Local search algorithms - Computer Science, Stony Brook University
... Local search: algorithms that perform local search in the state space, evaluating and modifying one or more current states rather than systematically exploring paths from an initial state. ♦ Operate using a single (or few) current node and gererally move only to neighbors of the node. ♦ Paths follow ...
... Local search: algorithms that perform local search in the state space, evaluating and modifying one or more current states rather than systematically exploring paths from an initial state. ♦ Operate using a single (or few) current node and gererally move only to neighbors of the node. ♦ Paths follow ...
Math 105 Week 11 March 21, 2011 1. Lesson plan
... 1.1. Section 12.9. An extremely important optimization problem with many real-life applications is one where, instead of finding local maxima or minima, one needs to identify largest or smallest values of a function subject to a certain number of rules or constraints. We will spend two lecture hours ...
... 1.1. Section 12.9. An extremely important optimization problem with many real-life applications is one where, instead of finding local maxima or minima, one needs to identify largest or smallest values of a function subject to a certain number of rules or constraints. We will spend two lecture hours ...
Chapter 12: Copying with the Limitations of Algorithm Power
... • Time efficiency: O(knk+1) • There are fully polynomial schemes: algorithms with polynomial running time as functions of both n and k ...
... • Time efficiency: O(knk+1) • There are fully polynomial schemes: algorithms with polynomial running time as functions of both n and k ...