Title Goes Here - Binus Repository
... 6. Distributivity of scalar sums: 7. Distributivity of vector sums: ...
... 6. Distributivity of scalar sums: 7. Distributivity of vector sums: ...
Assignment 4
... An open interval in R is of the form (a, b), where −∞ ≤ a < b ≤ +∞. (1) Let X, Y, Z be smooth vector fields on a smooth manifold. Verify the Jacobi identity: [X, [Y, Z]] + [Y, [Z, X]] + [Z, [X, Y ]] = 0. (2) Let X be a smooth vector field on a smooth manifold M , and let γ : I → M be a nonconstant i ...
... An open interval in R is of the form (a, b), where −∞ ≤ a < b ≤ +∞. (1) Let X, Y, Z be smooth vector fields on a smooth manifold. Verify the Jacobi identity: [X, [Y, Z]] + [Y, [Z, X]] + [Z, [X, Y ]] = 0. (2) Let X be a smooth vector field on a smooth manifold M , and let γ : I → M be a nonconstant i ...
LINEAR ALGEBRA. Part 0 Definitions. Let F stands for R, or C, or
... linearly independent subsets in it The rank of a linear map is defined as the dimension of its range (which is a subspace in the target space, and is therefore a vector space on its own). 1. Show that every linear map Fn → Fm is the multiplication by an m × nmatrix, A: x 7→ Ax. 2. Prove that in Fn , ...
... linearly independent subsets in it The rank of a linear map is defined as the dimension of its range (which is a subspace in the target space, and is therefore a vector space on its own). 1. Show that every linear map Fn → Fm is the multiplication by an m × nmatrix, A: x 7→ Ax. 2. Prove that in Fn , ...
Document
... If A is an m×n matrix with linearly independent column vectors, then for every m×1 matrix b, the linear system Ax = b has a unique least squares solution. This solution is given by x ( A A) 1 Ab Moreover, if W is the column space of A, then the orthogonal projection of b on W is projW b Ax ...
... If A is an m×n matrix with linearly independent column vectors, then for every m×1 matrix b, the linear system Ax = b has a unique least squares solution. This solution is given by x ( A A) 1 Ab Moreover, if W is the column space of A, then the orthogonal projection of b on W is projW b Ax ...
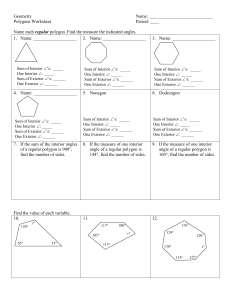
Geometry Name: Polygons Worksheet Period: ____ Name each
... 28. Note: You can’t use the Triangle Exterior Angle Theorem with the given information. You should use the Vertical Angle Theorem and the Triangle Sum Theorem. ...
... 28. Note: You can’t use the Triangle Exterior Angle Theorem with the given information. You should use the Vertical Angle Theorem and the Triangle Sum Theorem. ...
Vector Spaces: 3.1 • A set is a collection of objects. Usually the
... • A set is a collection of objects. Usually the objects in a set share some common features. For example the set of all m by n matrices can be given a name such as Mmn and described by Mmn = {A : A is an m x n matrix} This is stated: ”The set M ’sub’ m n is the set of all A such that A is an m by n ...
... • A set is a collection of objects. Usually the objects in a set share some common features. For example the set of all m by n matrices can be given a name such as Mmn and described by Mmn = {A : A is an m x n matrix} This is stated: ”The set M ’sub’ m n is the set of all A such that A is an m by n ...
PDF
... For any subset R ⊆ B and any x, y ∈ V , define the cylindrification of R by Cx (R) := {p ∈ AV | ∃r ∈ R such that r(y) = p(y) for any y 6= x}, and the diagonal set by Dxy = {p ∈ AV | p(x) = p(y)}. Now, define ∃ : V → B B and d : V × V → B by ∃x = Cx and dxy = Dxy . Proposition 2. (B, V, ∃, d) is a cy ...
... For any subset R ⊆ B and any x, y ∈ V , define the cylindrification of R by Cx (R) := {p ∈ AV | ∃r ∈ R such that r(y) = p(y) for any y 6= x}, and the diagonal set by Dxy = {p ∈ AV | p(x) = p(y)}. Now, define ∃ : V → B B and d : V × V → B by ∃x = Cx and dxy = Dxy . Proposition 2. (B, V, ∃, d) is a cy ...
FMM CMSC 878R/AMSC 698R Lecture 6
... • Limit can lie within the space or outside it. IF limits of all convergent sequences inside converge to an element of the space, it is complete. • Rational numbers are incomplete – Transcedentals can be defined as limits of rational ...
... • Limit can lie within the space or outside it. IF limits of all convergent sequences inside converge to an element of the space, it is complete. • Rational numbers are incomplete – Transcedentals can be defined as limits of rational ...
USE OF LINEAR ALGEBRA I Math 21b, O. Knill
... useful or relevant. The aim is to convince you that it is worth learning this subject. Most likely, some of this handout does not make much sense yet to you. Look at this page at the end of the course again, some of the content will become more interesting then. ...
... useful or relevant. The aim is to convince you that it is worth learning this subject. Most likely, some of this handout does not make much sense yet to you. Look at this page at the end of the course again, some of the content will become more interesting then. ...
Math 5A: Homework #10 Solution
... 52. The first quadrant is closed under addition but not scalar multiplication. Any vector in the first quadrant can be expressed (x, y) where x > 0 and y > 0. Adding any two vectors of this form, we get (x, y) + (z, t) = (x + z, y + t) and x + z > 0 since x, z > 0 and y + t > 0, since y, t > 0. So t ...
... 52. The first quadrant is closed under addition but not scalar multiplication. Any vector in the first quadrant can be expressed (x, y) where x > 0 and y > 0. Adding any two vectors of this form, we get (x, y) + (z, t) = (x + z, y + t) and x + z > 0 since x, z > 0 and y + t > 0, since y, t > 0. So t ...
General history of algebra
... operation (there are negative number) • Multiplication isn’t necessarily commutative and it doesn’t have an inverse (there’s no division) • Multiplication distributes over addition • Examples: rationals, reals under these limits 3 (4 + 5) = 12 + 8, but 12 + 8 ≠ 8 + 12 ...
... operation (there are negative number) • Multiplication isn’t necessarily commutative and it doesn’t have an inverse (there’s no division) • Multiplication distributes over addition • Examples: rationals, reals under these limits 3 (4 + 5) = 12 + 8, but 12 + 8 ≠ 8 + 12 ...
11.1 Three-Dimensional Coordinate System
... For example, a = h4, −3, 6i is parallel to b = − 34 , 1, −2 since a = −3b. Given two vectors a = ha1 , a2 , a3 i and b = hb1 , b2 , b3 i, the dot product (or scalar product) of a and b, denoted a · b, can be found in either of the following ways: a · b = |a||b| cos θ where θ is the angle between a a ...
... For example, a = h4, −3, 6i is parallel to b = − 34 , 1, −2 since a = −3b. Given two vectors a = ha1 , a2 , a3 i and b = hb1 , b2 , b3 i, the dot product (or scalar product) of a and b, denoted a · b, can be found in either of the following ways: a · b = |a||b| cos θ where θ is the angle between a a ...
aa9pdf
... 1. Let A be a finitely generated C-algebra and let a ∈ A be a nonalgebraic element. Show that there are uncountably many λ ∈ C such that the element a − λ is not a zero divisor but, at the same time, it is not invertible. (Thus, as opposed to the case of finite dimensional algebras, ‘most’ of noninv ...
... 1. Let A be a finitely generated C-algebra and let a ∈ A be a nonalgebraic element. Show that there are uncountably many λ ∈ C such that the element a − λ is not a zero divisor but, at the same time, it is not invertible. (Thus, as opposed to the case of finite dimensional algebras, ‘most’ of noninv ...
Lecture 9: 3.2 Norm of a Vector
... a specified nonzero vector a and the other perpendicular to a. We have w2 = u –w1 and w1 + w2 = w1 + (u –w1) = u The vector w1 is called the orthogonal projection (正交投影) of u on a or sometimes the vector component (分向量) of u along a, and denoted by projau The vector w2 is called the vector component ...
... a specified nonzero vector a and the other perpendicular to a. We have w2 = u –w1 and w1 + w2 = w1 + (u –w1) = u The vector w1 is called the orthogonal projection (正交投影) of u on a or sometimes the vector component (分向量) of u along a, and denoted by projau The vector w2 is called the vector component ...
Division algebras
... B × in an essential way by considering the action by conjugation on itself and using the orbit-stabilizer formula. Finally, we give some examples of division algebras. Naturally, our most interesting examples will be the ones where A is a field. • Finite fields Fq with q a prime power (as in the abo ...
... B × in an essential way by considering the action by conjugation on itself and using the orbit-stabilizer formula. Finally, we give some examples of division algebras. Naturally, our most interesting examples will be the ones where A is a field. • Finite fields Fq with q a prime power (as in the abo ...
JAIPUR NATIONAL UNIVERSITY, JAIPUR
... What is the fundamental difference between a function and a relation? ...
... What is the fundamental difference between a function and a relation? ...
Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogs. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation of their boundaries—a choice of clockwise or counterclockwise.When regarded in this manner, the exterior product of two vectors is called a 2-blade. More generally, the exterior product of any number k of vectors can be defined and is sometimes called a k-blade. It lives in a space known as the kth exterior power. The magnitude of the resulting k-blade is the volume of the k-dimensional parallelotope whose edges are the given vectors, just as the magnitude of the scalar triple product of vectors in three dimensions gives the volume of the parallelepiped generated by those vectors.The exterior algebra, or Grassmann algebra after Hermann Grassmann, is the algebraic system whose product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, blades have a concrete geometric interpretation, and objects in the exterior algebra can be manipulated according to a set of unambiguous rules. The exterior algebra contains objects that are not just k-blades, but sums of k-blades; such a sum is called a k-vector. The k-blades, because they are simple products of vectors, are called the simple elements of the algebra. The rank of any k-vector is defined to be the smallest number of simple elements of which it is a sum. The exterior product extends to the full exterior algebra, so that it makes sense to multiply any two elements of the algebra. Equipped with this product, the exterior algebra is an associative algebra, which means that α ∧ (β ∧ γ) = (α ∧ β) ∧ γ for any elements α, β, γ. The k-vectors have degree k, meaning that they are sums of products of k vectors. When elements of different degrees are multiplied, the degrees add like multiplication of polynomials. This means that the exterior algebra is a graded algebra.The definition of the exterior algebra makes sense for spaces not just of geometric vectors, but of other vector-like objects such as vector fields or functions. In full generality, the exterior algebra can be defined for modules over a commutative ring, and for other structures of interest in abstract algebra. It is one of these more general constructions where the exterior algebra finds one of its most important applications, where it appears as the algebra of differential forms that is fundamental in areas that use differential geometry. Differential forms are mathematical objects that represent infinitesimal areas of infinitesimal parallelograms (and higher-dimensional bodies), and so can be integrated over surfaces and higher dimensional manifolds in a way that generalizes the line integrals from calculus. The exterior algebra also has many algebraic properties that make it a convenient tool in algebra itself. The association of the exterior algebra to a vector space is a type of functor on vector spaces, which means that it is compatible in a certain way with linear transformations of vector spaces. The exterior algebra is one example of a bialgebra, meaning that its dual space also possesses a product, and this dual product is compatible with the exterior product. This dual algebra is precisely the algebra of alternating multilinear forms, and the pairing between the exterior algebra and its dual is given by the interior product.





![1. Let A = 1 −1 1 1 0 −1 2 1 1 . a) [2 marks] Find the](http://s1.studyres.com/store/data/005284378_1-9abef9398f6a7d24059a09f56fe1ac13-300x300.png)