Midterm 2 solutions
... Solution: Let R = R. Since R is a field the only proper ideal is the zero ideal, so it has no nonzero prime ideals. 2. Let F = R and V be the vector space of polynomials in x over R of degree at most n. (a) (5 points) What is dim V ⊗ V ? dim V ∧ V ? Solution: V has a basis 1, x, . . . , xn ; thus V ...
... Solution: Let R = R. Since R is a field the only proper ideal is the zero ideal, so it has no nonzero prime ideals. 2. Let F = R and V be the vector space of polynomials in x over R of degree at most n. (a) (5 points) What is dim V ⊗ V ? dim V ∧ V ? Solution: V has a basis 1, x, . . . , xn ; thus V ...
Vector Spaces
... The set of integers Z and the set of rational numbers Q are commutative groups under normal addition. But the set of natural numbers ℵ is not a group because there are no additive inverses in ℵ and there is no zero element. The following theorem holds for any group V , in particular for a vector spa ...
... The set of integers Z and the set of rational numbers Q are commutative groups under normal addition. But the set of natural numbers ℵ is not a group because there are no additive inverses in ℵ and there is no zero element. The following theorem holds for any group V , in particular for a vector spa ...
Dot Product, Cross Product, Determinants
... the negative of the other. We will see below that the three vectors ~a,~b,~x should have “positive orientation” in the sense of the “right hand rule”: If the thumb of the right hand points in the direction of ~a, the index finger in the direction of ~b, then ~x points in the direction given by the m ...
... the negative of the other. We will see below that the three vectors ~a,~b,~x should have “positive orientation” in the sense of the “right hand rule”: If the thumb of the right hand points in the direction of ~a, the index finger in the direction of ~b, then ~x points in the direction given by the m ...
Solution Set - Harvard Math Department
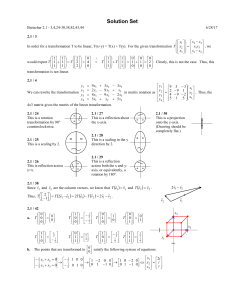
... a. We can show that transformation T is linear by finding a matrix of T. Recalling the definition of matrix multiplication, the formula for T is similar to the matrix multiplication of a row vector by a column vector. In fact, the row vector is ...
... a. We can show that transformation T is linear by finding a matrix of T. Recalling the definition of matrix multiplication, the formula for T is similar to the matrix multiplication of a row vector by a column vector. In fact, the row vector is ...
Practice Exam 2
... where, u1 + u2 ∈ H because H is a subspace, thus closed under addition; and v1 + v2 ∈ K similarly. This shows that w1 + w2 can be written as the sum of two vectors, one in H and the other in K. So, again by definition, w1 + w2 ∈ H + K, namely, H + K is closed under addition. For scalar multiplicatio ...
... where, u1 + u2 ∈ H because H is a subspace, thus closed under addition; and v1 + v2 ∈ K similarly. This shows that w1 + w2 can be written as the sum of two vectors, one in H and the other in K. So, again by definition, w1 + w2 ∈ H + K, namely, H + K is closed under addition. For scalar multiplicatio ...
Hopf algebras in renormalisation for Encyclopædia of Mathematics
... The renormalisation procedure is an algorithm of combinatorial nature, the BPHZ algorithm (after N. Bogoliubov, O. Parasiuk, K. Hepp and W. Zimmermann). The combinatorial objects involved are Feynman graphs: to each graph3 corresponds (by Feynman rules) a quantity to be renormalised, and an integer ...
... The renormalisation procedure is an algorithm of combinatorial nature, the BPHZ algorithm (after N. Bogoliubov, O. Parasiuk, K. Hepp and W. Zimmermann). The combinatorial objects involved are Feynman graphs: to each graph3 corresponds (by Feynman rules) a quantity to be renormalised, and an integer ...
The Heisenberg Algebra
... The group Sp(2n, R) is non-compact, but we can try and produce a projective representation of it using an analogous construction to the one used to produce the projective spinor representation of SO(2n). This infinite dimensional representation will be called the metaplectic representation and the ^ ...
... The group Sp(2n, R) is non-compact, but we can try and produce a projective representation of it using an analogous construction to the one used to produce the projective spinor representation of SO(2n). This infinite dimensional representation will be called the metaplectic representation and the ^ ...
Vector Spaces and Linear Maps
... Exercise 14.18. Find a basis for R2 that contains none of the standard basis vectors, nor any scalar multiple of them. Can you do the same for R3 ? Proposition 14.19. If x1 , . . . , xn is a sequence of vectors in V , the following are equivalent. 1. The sequence x1 , . . . , xn is linearly dependen ...
... Exercise 14.18. Find a basis for R2 that contains none of the standard basis vectors, nor any scalar multiple of them. Can you do the same for R3 ? Proposition 14.19. If x1 , . . . , xn is a sequence of vectors in V , the following are equivalent. 1. The sequence x1 , . . . , xn is linearly dependen ...
Algebra IB - Santa Rosa District Schools, Florida
... Use the zero product property of real numbers in a variety of contexts to identify solutions to equations. ...
... Use the zero product property of real numbers in a variety of contexts to identify solutions to equations. ...
the volume of a region defined by polynomial inequalities 265
... Let C be the closed convex cone in Rn generated by the cv, i.e., the elements of C are all linear combinations piCx+p2c2+- ■■+pkck with p^O. Let ( , ) be the usual inner product in R", and let C* be the dual cone to C with respect to this scalar product; i.e., C* is the set of y e Rn such that (y, x ...
... Let C be the closed convex cone in Rn generated by the cv, i.e., the elements of C are all linear combinations piCx+p2c2+- ■■+pkck with p^O. Let ( , ) be the usual inner product in R", and let C* be the dual cone to C with respect to this scalar product; i.e., C* is the set of y e Rn such that (y, x ...
Linear Algebra - Taleem-E
... A subset W of a vector space V is called a subspace of V if W itself is a vector space under the addition and scalar multiplication defined on V. ...
... A subset W of a vector space V is called a subspace of V if W itself is a vector space under the addition and scalar multiplication defined on V. ...
HURWITZ` THEOREM 1. Introduction In this article we describe
... In this article we describe several results based on the paper [Hur98] and which we will refer to as Hurwitz’ theorem. There are several related results: the classification of real normed division algebras, the classification of complex composition algebras and the classification of real composition ...
... In this article we describe several results based on the paper [Hur98] and which we will refer to as Hurwitz’ theorem. There are several related results: the classification of real normed division algebras, the classification of complex composition algebras and the classification of real composition ...
Linear Algebra Vocabulary Homework
... To get you started and to clarify the question, I have included answers to several of the questions. Your homework should include answers to every question, including the ones where I provided answers. You’re allowed to copy my answers, but if you do, make sure to understand what they mean, and why ...
... To get you started and to clarify the question, I have included answers to several of the questions. Your homework should include answers to every question, including the ones where I provided answers. You’re allowed to copy my answers, but if you do, make sure to understand what they mean, and why ...
Representation theory of finite groups
... from k to the ring EndAb (M ) of group homomorphisms M → M . If you have never seen this before, please take a moment and convince yourself that within this concise statement is encoded the entire list of vector space axioms. The following definition is therefore nothing surprising. Let R be a ring. ...
... from k to the ring EndAb (M ) of group homomorphisms M → M . If you have never seen this before, please take a moment and convince yourself that within this concise statement is encoded the entire list of vector space axioms. The following definition is therefore nothing surprising. Let R be a ring. ...
Document
... 1) The set of all real-coefficient polynomials of degree three, together with usual addition and multiplication, is not a vector space. 2) The set of all rational numbers with standard addition and multiplication is a not vector space. However, the set of all real numbers (complex numbers), with sta ...
... 1) The set of all real-coefficient polynomials of degree three, together with usual addition and multiplication, is not a vector space. 2) The set of all rational numbers with standard addition and multiplication is a not vector space. However, the set of all real numbers (complex numbers), with sta ...
Math 700 Homework 3 Solutions Question 1. Let T : V → W and S
... where each ci ∈ F and all but finitely many of the ci are zero.) Let T (c1 , c2 , c3 , . . . ) = (0, c1 , c2 , c3 , . . . ) and S(c1 , c2 , c3 , . . . ) = (c2 , c3 , . . . ) . Once again, ST is the identity map, T is one-to-one, but T is not onto. Question 2. Let V be a vector space over the field F ...
... where each ci ∈ F and all but finitely many of the ci are zero.) Let T (c1 , c2 , c3 , . . . ) = (0, c1 , c2 , c3 , . . . ) and S(c1 , c2 , c3 , . . . ) = (c2 , c3 , . . . ) . Once again, ST is the identity map, T is one-to-one, but T is not onto. Question 2. Let V be a vector space over the field F ...
Class 43: Andrew Healy - Rational Homotopy Theory
... It is well-known that the homotopy groups of spaces with simple CW-decompositions are difficult to compute. Since it is known that πn (X) is a finitely generated abelian group for n ≥ 2, the computation of πn (X) can be broken into two parts: computing the rank of πn (X) and computing the torsion of ...
... It is well-known that the homotopy groups of spaces with simple CW-decompositions are difficult to compute. Since it is known that πn (X) is a finitely generated abelian group for n ≥ 2, the computation of πn (X) can be broken into two parts: computing the rank of πn (X) and computing the torsion of ...
Lecture notes
... Two matrices can be multiplied together, if the number of columns of the first matrix is equal to the number of rows of the second matrix. ...
... Two matrices can be multiplied together, if the number of columns of the first matrix is equal to the number of rows of the second matrix. ...
Linear Independence
... A set of vectors are linearly dependent if any of the following are true: 1. The set has two vectors and one is a multiple of the other. 2. The set has two or more vectors and one of the vectors is a linear combination of the others. ...
... A set of vectors are linearly dependent if any of the following are true: 1. The set has two vectors and one is a multiple of the other. 2. The set has two or more vectors and one of the vectors is a linear combination of the others. ...
Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogs. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation of their boundaries—a choice of clockwise or counterclockwise.When regarded in this manner, the exterior product of two vectors is called a 2-blade. More generally, the exterior product of any number k of vectors can be defined and is sometimes called a k-blade. It lives in a space known as the kth exterior power. The magnitude of the resulting k-blade is the volume of the k-dimensional parallelotope whose edges are the given vectors, just as the magnitude of the scalar triple product of vectors in three dimensions gives the volume of the parallelepiped generated by those vectors.The exterior algebra, or Grassmann algebra after Hermann Grassmann, is the algebraic system whose product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, blades have a concrete geometric interpretation, and objects in the exterior algebra can be manipulated according to a set of unambiguous rules. The exterior algebra contains objects that are not just k-blades, but sums of k-blades; such a sum is called a k-vector. The k-blades, because they are simple products of vectors, are called the simple elements of the algebra. The rank of any k-vector is defined to be the smallest number of simple elements of which it is a sum. The exterior product extends to the full exterior algebra, so that it makes sense to multiply any two elements of the algebra. Equipped with this product, the exterior algebra is an associative algebra, which means that α ∧ (β ∧ γ) = (α ∧ β) ∧ γ for any elements α, β, γ. The k-vectors have degree k, meaning that they are sums of products of k vectors. When elements of different degrees are multiplied, the degrees add like multiplication of polynomials. This means that the exterior algebra is a graded algebra.The definition of the exterior algebra makes sense for spaces not just of geometric vectors, but of other vector-like objects such as vector fields or functions. In full generality, the exterior algebra can be defined for modules over a commutative ring, and for other structures of interest in abstract algebra. It is one of these more general constructions where the exterior algebra finds one of its most important applications, where it appears as the algebra of differential forms that is fundamental in areas that use differential geometry. Differential forms are mathematical objects that represent infinitesimal areas of infinitesimal parallelograms (and higher-dimensional bodies), and so can be integrated over surfaces and higher dimensional manifolds in a way that generalizes the line integrals from calculus. The exterior algebra also has many algebraic properties that make it a convenient tool in algebra itself. The association of the exterior algebra to a vector space is a type of functor on vector spaces, which means that it is compatible in a certain way with linear transformations of vector spaces. The exterior algebra is one example of a bialgebra, meaning that its dual space also possesses a product, and this dual product is compatible with the exterior product. This dual algebra is precisely the algebra of alternating multilinear forms, and the pairing between the exterior algebra and its dual is given by the interior product.