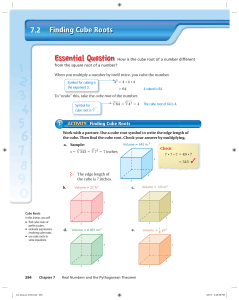
Solution
... Problem 3. Find all solutions of x12 ≡ 7 (mod 19) and x12 ≡ 6 (mod 19). Solution: We use the fact that 2 is a primitive root of 19 from the previous problem. Write x = 2k . Then because 7 ≡ 64 = 26 (mod 19) the first equation can be rewritten as 212k ≡ 26 (mod 19). This is equivalent to 18 | 12k − 6 ...
... Problem 3. Find all solutions of x12 ≡ 7 (mod 19) and x12 ≡ 6 (mod 19). Solution: We use the fact that 2 is a primitive root of 19 from the previous problem. Write x = 2k . Then because 7 ≡ 64 = 26 (mod 19) the first equation can be rewritten as 212k ≡ 26 (mod 19). This is equivalent to 18 | 12k − 6 ...
On the Sum of Square Roots of Polynomials and Related Problems
... Pn 1.1√(Lower bounding a non-zero ‘signed’ sum of square roots of integers). Given a sum S = i=1 δi · ai , where δi ∈ {+1, −1} and ai ’s are positive integers upper bounded by N , find a tight lower bound on |S| in terms of n and N when S 6= 0. Is it true that for a non-zero S, |S| ≥ 1/2poly(n,log N ...
... Pn 1.1√(Lower bounding a non-zero ‘signed’ sum of square roots of integers). Given a sum S = i=1 δi · ai , where δi ∈ {+1, −1} and ai ’s are positive integers upper bounded by N , find a tight lower bound on |S| in terms of n and N when S 6= 0. Is it true that for a non-zero S, |S| ≥ 1/2poly(n,log N ...
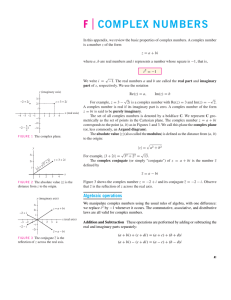
Root of unity
In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that gives 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.In field theory and ring theory the notion of root of unity also applies to any ring with a multiplicative identity element. Any algebraically closed field has exactly n nth roots of unity, if n is not divisible by the characteristic of the field.