Multiplying complex numbers
... since 6 arg(w) could be any multiple of 360° more than arg(z). For example, take z to be -1/2, the green dot in the figure to the right. Then |z| is 1/2, and arg(z) is 180°. Let w be a sixth root of z. Then (1) |w| is |z|1/6 which is about 0.89. Also, (2) the argument of z is arg(z) = 180°. But the ...
... since 6 arg(w) could be any multiple of 360° more than arg(z). For example, take z to be -1/2, the green dot in the figure to the right. Then |z| is 1/2, and arg(z) is 180°. Let w be a sixth root of z. Then (1) |w| is |z|1/6 which is about 0.89. Also, (2) the argument of z is arg(z) = 180°. But the ...
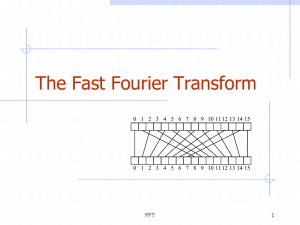
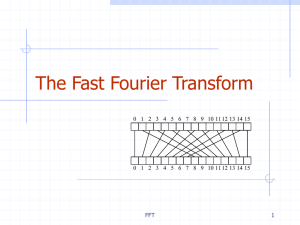
FFT - Personal Web Pages
... Given N-bit integers I and J, compute IJ. Assume: we can multiply words of O(log N) bits in constant time. Setup: Find a prime p=cn+1 that can be represented in one word, and set m=(log p)/3, so that we can view I and J as n-length vectors of m-bit words. Finding a primitive root of unity. ...
... Given N-bit integers I and J, compute IJ. Assume: we can multiply words of O(log N) bits in constant time. Setup: Find a prime p=cn+1 that can be represented in one word, and set m=(log p)/3, so that we can view I and J as n-length vectors of m-bit words. Finding a primitive root of unity. ...
solving polynomial equations by radicals31
... By the proof above, we know that it is impossible to solve all quintics by radicals, and thus no general solution can be found. However, there are many cases of quintics which are solvable by radicals. A case will be discussed below. a. Cyclotomic Polynomials Consider the cyclotomic polynomial ...
... By the proof above, we know that it is impossible to solve all quintics by radicals, and thus no general solution can be found. However, there are many cases of quintics which are solvable by radicals. A case will be discussed below. a. Cyclotomic Polynomials Consider the cyclotomic polynomial ...
Root of unity
In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that gives 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.In field theory and ring theory the notion of root of unity also applies to any ring with a multiplicative identity element. Any algebraically closed field has exactly n nth roots of unity, if n is not divisible by the characteristic of the field.