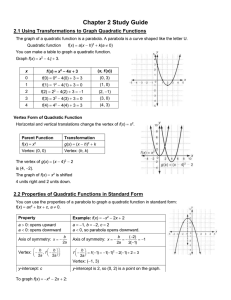
Chapter 2 Study Guide
... The discriminant of ax2 bx c 0 a 0 is b2 4ac. Use the discriminant to determine the number of roots of a quadratic equation. A quadratic equation can have 2 real solutions, 1 real solution, or 2 complex solutions. Find the type and number of solutions. x2 10x 25 ...
... The discriminant of ax2 bx c 0 a 0 is b2 4ac. Use the discriminant to determine the number of roots of a quadratic equation. A quadratic equation can have 2 real solutions, 1 real solution, or 2 complex solutions. Find the type and number of solutions. x2 10x 25 ...
Section 4: Complex Numbers Revision Material
... Real numbers relate to our normal world of experience. The square root of 4 is plus or minus 2 and the square root of 17 is plus or minus 4.1231 to four places of decimals. What is the square root of -17? The square roots of negative numbers can be interpreted by defining the square root of -1 to be ...
... Real numbers relate to our normal world of experience. The square root of 4 is plus or minus 2 and the square root of 17 is plus or minus 4.1231 to four places of decimals. What is the square root of -17? The square roots of negative numbers can be interpreted by defining the square root of -1 to be ...
Name: Cubes and Cube Roots: Note sheet How to Cube a Number
... Example: What is the cube root of 30? 1. If you know what perfect cube roots are around the number that will help you narrow your search. So what perfect cube is close to 30? 27-which has a root of 3 so you know you should start with numbers bigger than three. (You know it’s not 4 because 4x4x4=64) ...
... Example: What is the cube root of 30? 1. If you know what perfect cube roots are around the number that will help you narrow your search. So what perfect cube is close to 30? 27-which has a root of 3 so you know you should start with numbers bigger than three. (You know it’s not 4 because 4x4x4=64) ...
Root of unity
In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that gives 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.In field theory and ring theory the notion of root of unity also applies to any ring with a multiplicative identity element. Any algebraically closed field has exactly n nth roots of unity, if n is not divisible by the characteristic of the field.