a generalization of the differential approach to recursive query
... The differential (or seminaive) approach to query evaluation is described in [2], [3], (51. Focusing on the naive bottom-up method of evaluation, the approach eliminates some of the obviously redundant joins. However, “the problem is not solved in its entirety and only a number of transformations ar ...
... The differential (or seminaive) approach to query evaluation is described in [2], [3], (51. Focusing on the naive bottom-up method of evaluation, the approach eliminates some of the obviously redundant joins. However, “the problem is not solved in its entirety and only a number of transformations ar ...
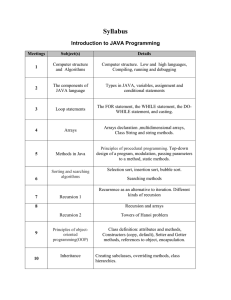
Week 6 Questions
... the calling function to indicate if the given string is palindrome or not. You can assume that the string has only characters from the set {a-z, A-Z}. Note that: – palindrome(X) = true, if |X| < 2 – palindrome(aXa) = palindrome(X), if |X| >= 2 ...
... the calling function to indicate if the given string is palindrome or not. You can assume that the string has only characters from the set {a-z, A-Z}. Note that: – palindrome(X) = true, if |X| < 2 – palindrome(aXa) = palindrome(X), if |X| >= 2 ...
Binary Search
... } else if (K==A[Midpoint]){ return Midpoint; } else if (K > A[Midpoint]){ return BinarySearch(K, Midpoint+1, R); ...
... } else if (K==A[Midpoint]){ return Midpoint; } else if (K > A[Midpoint]){ return BinarySearch(K, Midpoint+1, R); ...
Recursion
... • Recursive function - invokes itself directly or indirectly – direct recursion - function is invoked by a statement in its own body – indirect recursion - one function initiates a sequence of function invocations that eventually invokes the original ...
... • Recursive function - invokes itself directly or indirectly – direct recursion - function is invoked by a statement in its own body – indirect recursion - one function initiates a sequence of function invocations that eventually invokes the original ...
CS112 Lecture: Recursion Last revised 3/20/08 1. Von Koch curve images
... composed of constants, the variable X, and the arithmetic operators +, (unary and binary), *, and /. 1. Example: (3 * (- X)) a) Base case: a constant, by itself, is an arithmetic expression. Example: 3 is an arithmetic expression. b) Another base case: a variable, by itself, is an arithmetic express ...
... composed of constants, the variable X, and the arithmetic operators +, (unary and binary), *, and /. 1. Example: (3 * (- X)) a) Base case: a constant, by itself, is an arithmetic expression. Example: 3 is an arithmetic expression. b) Another base case: a variable, by itself, is an arithmetic express ...
pdf
... example of how challenging it is to include all computation in the object theory. It is also key to including unsolvability results with a minimum effort; the halting problem and related concepts are fundamentally about whether computations converge, and in type theory this is the essence of ...
... example of how challenging it is to include all computation in the object theory. It is also key to including unsolvability results with a minimum effort; the halting problem and related concepts are fundamentally about whether computations converge, and in type theory this is the essence of ...
COS_470-Practice-Week_05YanaAleksieva
... ;; construct a list with the first element from nums and ;; the result of ;; calling the insert1 function with num and the rest of ;;nums (cdr nums) ...
... ;; construct a list with the first element from nums and ;; the result of ;; calling the insert1 function with num and the rest of ;;nums (cdr nums) ...
Smart programming languages, smart program analysis
... Total Functional Programming Total Functional Programming In total functional programming paradigm all programs are terminating. In particular, there is no general recursion. Instead, only some restricted forms of recursion are allowed, which are guaranteed to terminate. Usually, these are simple i ...
... Total Functional Programming Total Functional Programming In total functional programming paradigm all programs are terminating. In particular, there is no general recursion. Instead, only some restricted forms of recursion are allowed, which are guaranteed to terminate. Usually, these are simple i ...
review1
... 2. When using the method System.out.printf( ), what is the purpose of the %d format code? 3. What does it mean for the return type of a method to be void? 4. What Java keyword is used when invoking a constructor? 5. Suppose a is a one-dimensional array of double. Fill in the blanks in the following ...
... 2. When using the method System.out.printf( ), what is the purpose of the %d format code? 3. What does it mean for the return type of a method to be void? 4. What Java keyword is used when invoking a constructor? 5. Suppose a is a one-dimensional array of double. Fill in the blanks in the following ...
An Introduction to F# – Sushant Bhatia
... execution path that led to the call Functions are first-class values (viewed as values themselves, computed by other functions and can be parameters to functions) ...
... execution path that led to the call Functions are first-class values (viewed as values themselves, computed by other functions and can be parameters to functions) ...
ppt
... • If you know a set of statements are true, what other statements can you also deduce are true? • If I tell you that all men are mortal, and Socrates is a man, what can you deduce? ...
... • If you know a set of statements are true, what other statements can you also deduce are true? • If I tell you that all men are mortal, and Socrates is a man, what can you deduce? ...
ppt - Dr. Wissam Fawaz
... // This method returns the sum of 1 to num // Refer to SumApp project public int sum (int num) ...
... // This method returns the sum of 1 to num // Refer to SumApp project public int sum (int num) ...
CS-2852 Data Structures
... • Some functional programming languages don’t have loops (equivalent to imperative looping constructs) • A function “calls itself” – directly or not CS-2852 Data Structures, Andrew J. Wozniewicz ...
... • Some functional programming languages don’t have loops (equivalent to imperative looping constructs) • A function “calls itself” – directly or not CS-2852 Data Structures, Andrew J. Wozniewicz ...
Recursion Review - Department of Computer Science
... if (n <= 0) return 0; else if (n == 1) return 1; else return fibonacci(n − 1) + fibonacci(n − 2); ...
... if (n <= 0) return 0; else if (n == 1) return 1; else return fibonacci(n − 1) + fibonacci(n − 2); ...
Problem Set 2
... 3. Give an example of a program than runs faster if ran lazily, and one that runs faster if ran eagerly. 4. Give an “interesting” example of a program that uses dynamic scoping to modify its behavior at runtime (using the Y combinator for example, or using a f ix that computes as follows f ix(F ) → ...
... 3. Give an example of a program than runs faster if ran lazily, and one that runs faster if ran eagerly. 4. Give an “interesting” example of a program that uses dynamic scoping to modify its behavior at runtime (using the Y combinator for example, or using a f ix that computes as follows f ix(F ) → ...
Lecture
... Recursion is a repetitive process in which an algorithm calls itself. Usually recursion is organized in such a way that a subroutine calls itself or a function calls itself ...
... Recursion is a repetitive process in which an algorithm calls itself. Usually recursion is organized in such a way that a subroutine calls itself or a function calls itself ...
Recursion
... completely before the control goes back to the previous call. The execution in the previous call begins from the point immediately following the recursive call. A recursive function in which the last statement executed is the recursive call is called a tail recursive function. ...
... completely before the control goes back to the previous call. The execution in the previous call begins from the point immediately following the recursive call. A recursive function in which the last statement executed is the recursive call is called a tail recursive function. ...
Deployment of Sensing Devices on Critical Infrastructure
... Recursion is a repetitive process in which an algorithm calls itself. Usually recursion is organized in such a way that a subroutine calls itself or a function calls itself ...
... Recursion is a repetitive process in which an algorithm calls itself. Usually recursion is organized in such a way that a subroutine calls itself or a function calls itself ...
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration). The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.""The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.""Most computer programming languages support recursion by allowing a function to call itself within the program text. Some functional programming languages do not define any looping constructs but rely solely on recursion to repeatedly call code. Computability theory proves that these recursive-only languages are Turing complete; they are as computationally powerful as Turing complete imperative languages, meaning they can solve the same kinds of problems as imperative languages even without iterative control structures such as “while” and “for”.