Conservation decision-making in large state spaces
... trying each of the actions defined in the MDP. Although SDP gives the optimal solution to conservation management questions in a stochastic world, its applicability has always been limited by the so-called curse of dimensionality. The curse of dimensionality is the problem that adding new state vari ...
... trying each of the actions defined in the MDP. Although SDP gives the optimal solution to conservation management questions in a stochastic world, its applicability has always been limited by the so-called curse of dimensionality. The curse of dimensionality is the problem that adding new state vari ...
HP 12C Statistics - rearranging items HP12C Statistics
... The combination of ordered subgroups of a specific number of r items separated from a larger group with n items allows determining another number of different events that can be observed. The permutation formula shown in figure 2 below indicates the ordered permutations of n items taken r at a time. ...
... The combination of ordered subgroups of a specific number of r items separated from a larger group with n items allows determining another number of different events that can be observed. The permutation formula shown in figure 2 below indicates the ordered permutations of n items taken r at a time. ...
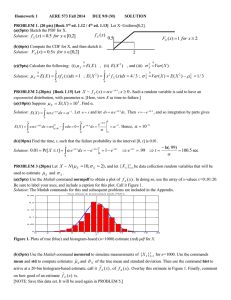
SOLUTION FOR HOMEWORK 8, STAT 4372 Welcome to your 8th
... Welcome to your 8th homework. Here you have an opportunity to solve classical estimation problems which are the must to solve on the exam due to their simplicity. 1. Problem 15.4 Given: X̄ = 35, 000, Sn = 75, 000, π̂50 = 10, 000, π̂90 = 100, 000. Using percentile matching for Weibull distribution, f ...
... Welcome to your 8th homework. Here you have an opportunity to solve classical estimation problems which are the must to solve on the exam due to their simplicity. 1. Problem 15.4 Given: X̄ = 35, 000, Sn = 75, 000, π̂50 = 10, 000, π̂90 = 100, 000. Using percentile matching for Weibull distribution, f ...
1 Review of Least Squares Solutions to Overdetermined Systems
... function to a data set. We can informally state the problem as follows: Problem 1.1 (Function Fitting). Given an interval [a, b] a function f : [a, b], and a parameter n, find a polynomial p ∈ Πn such that p ≈ f . We have seen how to solve this problem using interpolation, however, there are some im ...
... function to a data set. We can informally state the problem as follows: Problem 1.1 (Function Fitting). Given an interval [a, b] a function f : [a, b], and a parameter n, find a polynomial p ∈ Πn such that p ≈ f . We have seen how to solve this problem using interpolation, however, there are some im ...
Homework 1 SOLUTION
... PROBLEM 5 (10pts) Using the same data as was used in PROBLEM 3(b) above, view this data as associated with the 2D random variable (X,Y) which is the generation of two successive numbers using normrnd.m. Since each of these random variables is (marginally) the same as the 1-D random variable studied ...
... PROBLEM 5 (10pts) Using the same data as was used in PROBLEM 3(b) above, view this data as associated with the 2D random variable (X,Y) which is the generation of two successive numbers using normrnd.m. Since each of these random variables is (marginally) the same as the 1-D random variable studied ...
Sample Average Approximation of Expected Value Constrained
... also verified the effectiveness of the SAA approach for stochastic programs of the form (5). See [11] and references therein for further details. In this paper we investigate an SAA method for expected value constrained problems (1). We require the expected value constraint in (1) to be soft, i.e., ...
... also verified the effectiveness of the SAA approach for stochastic programs of the form (5). See [11] and references therein for further details. In this paper we investigate an SAA method for expected value constrained problems (1). We require the expected value constraint in (1) to be soft, i.e., ...
Quadrilaterals
... Greek philosopher who is considered the founder of Greek science, mathematics, and philosophy. He visited Egypt and probably Babylon, bringing back knowledge of astronomy and geometry. He invented deductive mathematics. To him is attributed Thales' theorem. Proclus attributed the following additiona ...
... Greek philosopher who is considered the founder of Greek science, mathematics, and philosophy. He visited Egypt and probably Babylon, bringing back knowledge of astronomy and geometry. He invented deductive mathematics. To him is attributed Thales' theorem. Proclus attributed the following additiona ...
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a mass and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items.The problem often arises in resource allocation where there are financial constraints and is studied in fields such as combinatorics, computer science, complexity theory, cryptography and applied mathematics.The knapsack problem has been studied for more than a century, with early works dating as far back as 1897. It is not known how the name ""knapsack problem"" originated, though the problem was referred to as such in the early works of mathematician Tobias Dantzig (1884–1956), suggesting that the name could have existed in folklore before a mathematical problem had been fully defined.