Exercises for the Lecture on Computational Number Theory
... the equation of an elliptic curve in Weierstrass normal form. Use this fact in order to show that given a prime p, one can construct an elliptic curve E(Fp ) together with a point P = (X, y) ∈ E without taking square roots. Hint: Start with X and an arbitrary elliptic curve, such that cY 2 = X 3 + a ...
... the equation of an elliptic curve in Weierstrass normal form. Use this fact in order to show that given a prime p, one can construct an elliptic curve E(Fp ) together with a point P = (X, y) ∈ E without taking square roots. Hint: Start with X and an arbitrary elliptic curve, such that cY 2 = X 3 + a ...
Document
... Use square root and cube root symbols to represent solutions to equations of the form x2 = p and x3 = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roots of small perfect cubes. Understand that a function from one set (called the domain) to another ...
... Use square root and cube root symbols to represent solutions to equations of the form x2 = p and x3 = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roots of small perfect cubes. Understand that a function from one set (called the domain) to another ...
Lecture 8 1 Equal-degree factoring over finite fields
... polynomial time algorithm. What about a deterministic algorithm? It turns out that if the finite field Fq is small in size (say, q = 5 or 7) then it is indeed possible to factor f deterministically 1 . This is done by reducing the equal-degree factoring problem to a root finding problem over Fq . We ...
... polynomial time algorithm. What about a deterministic algorithm? It turns out that if the finite field Fq is small in size (say, q = 5 or 7) then it is indeed possible to factor f deterministically 1 . This is done by reducing the equal-degree factoring problem to a root finding problem over Fq . We ...
Numbers and Polynomials (Handout January 20, 2012)
... (ii) real numbers are thought of as corresponding to points on the ‘real number line’. Both of these interpretations lend some useful intuition to the study of real numbers; but both interpretations are of limited value. Regarding (i), virtually none of the main properties of real numbers are easy c ...
... (ii) real numbers are thought of as corresponding to points on the ‘real number line’. Both of these interpretations lend some useful intuition to the study of real numbers; but both interpretations are of limited value. Regarding (i), virtually none of the main properties of real numbers are easy c ...
..
... . - transpose. Compute the rank and nullity of S. 5. Give n x n matrices over e that ha~e the following properties: i. the characteristic polynomial is (x + 1)4(x - i)Z ii. the minimal polynomial is (x + 1)2(x- i) iii. all have the same value for n and every nx n matrix over e that satisfies (i) and ...
... . - transpose. Compute the rank and nullity of S. 5. Give n x n matrices over e that ha~e the following properties: i. the characteristic polynomial is (x + 1)4(x - i)Z ii. the minimal polynomial is (x + 1)2(x- i) iii. all have the same value for n and every nx n matrix over e that satisfies (i) and ...
Evelyn Haley - Stony Brook Mathematics
... Question: Find the GCD of 1155 and 468 Various people used different methods with some using the Euclidean Algorithm. Formally the Euclidean Algorithm is Let m,n be integers and m>0. Then there exist integers q,r with 0≤r
... Question: Find the GCD of 1155 and 468 Various people used different methods with some using the Euclidean Algorithm. Formally the Euclidean Algorithm is Let m,n be integers and m>0. Then there exist integers q,r with 0≤r
FINITE FIELDS OF THE FORM GF(p)
... Modular Polynomial Arithmetic Let set S of polynomial coefficients is a finite field Zp, and polynomials have degree from 0 to n-1. There are totally pn different such polynomials. The definition consists of the following elements: 1. Arithmetic follows the ordinary rules of polynomial arithmetic u ...
... Modular Polynomial Arithmetic Let set S of polynomial coefficients is a finite field Zp, and polynomials have degree from 0 to n-1. There are totally pn different such polynomials. The definition consists of the following elements: 1. Arithmetic follows the ordinary rules of polynomial arithmetic u ...
FINITE FIELDS OF THE FORM GF(p)
... Modular Polynomial Arithmetic Let set S of polynomial coefficients is a finite field Zp, and polynomials have degree from 0 to n-1. There are totally pn different such polynomials. The definition consists of the following elements: 1. Arithmetic follows the ordinary rules of polynomial arithmetic u ...
... Modular Polynomial Arithmetic Let set S of polynomial coefficients is a finite field Zp, and polynomials have degree from 0 to n-1. There are totally pn different such polynomials. The definition consists of the following elements: 1. Arithmetic follows the ordinary rules of polynomial arithmetic u ...
Polynomials
... The degree of a polynomial is the highest x power in the expression. Add or subtract polynomials by column addition or subtraction, or by collecting like terms. Multiply polynomials using any method that helps you to remember to multiply every term in one expression by every term in the other. Solve ...
... The degree of a polynomial is the highest x power in the expression. Add or subtract polynomials by column addition or subtraction, or by collecting like terms. Multiply polynomials using any method that helps you to remember to multiply every term in one expression by every term in the other. Solve ...
Solutions to Exercises for Section 6
... The last part is asking whether there is a root of Y 2 + 1 = 0 in K; that is, is there an element of K whose square is −1(= 2)? One possibility is just to start checking, squaring the elements of K in turn, to see if 2 is a square in K. Alternatively, take a typical element aα + b, square it and rea ...
... The last part is asking whether there is a root of Y 2 + 1 = 0 in K; that is, is there an element of K whose square is −1(= 2)? One possibility is just to start checking, squaring the elements of K in turn, to see if 2 is a square in K. Alternatively, take a typical element aα + b, square it and rea ...
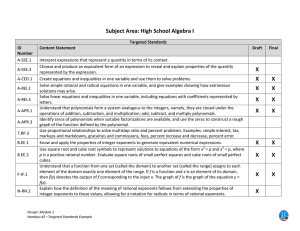
Algebra II – Unit 1 – Polynomial, Rational, and Radical Relationships
... a. A.SSE.1 Interpret expression that represent a quantity in terms of its context. i. Interpret parts of an expression, such as terms, factors, and coefficients. ii. Interpret complicated expressions by viewing one ore more of their parts as a single entity. b. A.SSE.2 Use the structure of an expres ...
... a. A.SSE.1 Interpret expression that represent a quantity in terms of its context. i. Interpret parts of an expression, such as terms, factors, and coefficients. ii. Interpret complicated expressions by viewing one ore more of their parts as a single entity. b. A.SSE.2 Use the structure of an expres ...
PDF
... Therefore if f and g are integer monic polynomials such that there g divides f over Q, that is there exists a polynomial h with rational coefficients such that f (X) = g(X)h(X), the g infact divides f over Z or h infact has only integer coefficients. Thus all the above divisions will only yeild int ...
... Therefore if f and g are integer monic polynomials such that there g divides f over Q, that is there exists a polynomial h with rational coefficients such that f (X) = g(X)h(X), the g infact divides f over Z or h infact has only integer coefficients. Thus all the above divisions will only yeild int ...
Polynomials - RutledgeMath2
... Reintroducing parts of polynomials and Operating with polynomials ...
... Reintroducing parts of polynomials and Operating with polynomials ...
Add & Subtract Polynomials
... rational and student has no success irrational partial with real numbers to write success with number and real number expressions. simplify expres expressions. sions based on contextual situations. -identify parts of an expression as related to the context and to each part ...
... rational and student has no success irrational partial with real numbers to write success with number and real number expressions. simplify expres expressions. sions based on contextual situations. -identify parts of an expression as related to the context and to each part ...