Minnesota State Colleges and Universities Intermediate Algebra Sample Questions
... equivalent. That is, the set of pairs (x, y) that satisfy 2 x − 6 y = 4 is equivalent to 10x − 30 y = 20. Therefore, the satisfy 10 x − ky = 20. The equation 2 x − 6 y = 20 and 10 x − ky = equations 10 x − 30 y = 20 are also equivalent. It follows that k = 30. ...
... equivalent. That is, the set of pairs (x, y) that satisfy 2 x − 6 y = 4 is equivalent to 10x − 30 y = 20. Therefore, the satisfy 10 x − ky = 20. The equation 2 x − 6 y = 20 and 10 x − ky = equations 10 x − 30 y = 20 are also equivalent. It follows that k = 30. ...
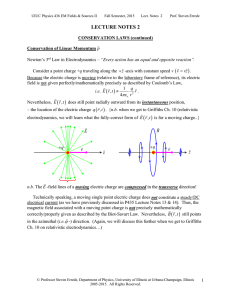
Lecture Notes 02: Conservation Laws (Continued): Conservation of Linear Momentum, Maxwell's Stress Tensor
... Thus, in electrodynamics, the electric charges and/or electric currents plus the electromagnetic ...
... Thus, in electrodynamics, the electric charges and/or electric currents plus the electromagnetic ...
Magnetic Field Interactions
... Lets now exam the path for a negatively charged particle moving through the same uniform magnetic field. The right hand rule shows us the direction of the cross product is also down. However, the negative sign included with the negative charge would reverse the direction of the force applied t ...
... Lets now exam the path for a negatively charged particle moving through the same uniform magnetic field. The right hand rule shows us the direction of the cross product is also down. However, the negative sign included with the negative charge would reverse the direction of the force applied t ...
Magnetism
... The meter shown here measures electric current. A magnet sitting in the coil of wire does not seem to do much. The meter reading is zero. No current is flowing. What if the magnet is moved back and forth? The meter’s needle swings away from zero. The moving magnet makes electricity that flows throug ...
... The meter shown here measures electric current. A magnet sitting in the coil of wire does not seem to do much. The meter reading is zero. No current is flowing. What if the magnet is moved back and forth? The meter’s needle swings away from zero. The moving magnet makes electricity that flows throug ...
Document
... If there is a plasma present in the space in front of the final optics mirrors • Aerosols are charged negatively and move to the location of highest potential • In etching reactors (for the semiconductor industry), accumulation of aerosols somewhere in between electrodes • As long as there is a plas ...
... If there is a plasma present in the space in front of the final optics mirrors • Aerosols are charged negatively and move to the location of highest potential • In etching reactors (for the semiconductor industry), accumulation of aerosols somewhere in between electrodes • As long as there is a plas ...
Lecture 4 Electric potential
... • V is a scalar not a vector. Simplifies solving problems. • We are free to choose V to be 0 at any location. Normally V is chosen to be 0 at the negative terminal of a battery or 0 at infinity for a point charge. ...
... • V is a scalar not a vector. Simplifies solving problems. • We are free to choose V to be 0 at any location. Normally V is chosen to be 0 at the negative terminal of a battery or 0 at infinity for a point charge. ...
Document
... The magnetic field lines around a long wire which carries an electric current form concentric circles around the wire. The direction of the magnetic field is perpendicular to the wire and is in the direction the fingers of your right hand would curl if you wrapped them around the wire with your thum ...
... The magnetic field lines around a long wire which carries an electric current form concentric circles around the wire. The direction of the magnetic field is perpendicular to the wire and is in the direction the fingers of your right hand would curl if you wrapped them around the wire with your thum ...
PSI AP 2 EMF Worksheet
... A. Increase the magnitude of the magnetic field that passes outside the loop B. Increase the magnitude of the magnetic field that passes through the loop. C. Increase the cross sectional area of the loop. D. Orient the loop so its normal vector is perpendicular to the external magnetic field directi ...
... A. Increase the magnitude of the magnetic field that passes outside the loop B. Increase the magnitude of the magnetic field that passes through the loop. C. Increase the cross sectional area of the loop. D. Orient the loop so its normal vector is perpendicular to the external magnetic field directi ...
ppt - plutonium
... Note that the surface does not have to be made of real matter – it is a surface that we can imagine, but that does not have to exist in reality. This kind of imaginary surface is called a Gaussian surface. We can imagine it to be any shape we want; it is very useful to choose one that makes the prob ...
... Note that the surface does not have to be made of real matter – it is a surface that we can imagine, but that does not have to exist in reality. This kind of imaginary surface is called a Gaussian surface. We can imagine it to be any shape we want; it is very useful to choose one that makes the prob ...
Chapter 13 Maxwell’s Equations and Electromagnetic Waves
... electric field produces a magnetic field. If so, then the right-hand side of Eq. (13.1.1) will have to be modified to reflect such “symmetry” between E and B . To see how magnetic fields can be created by a time-varying electric field, consider a capacitor which is being charged. During the charging ...
... electric field produces a magnetic field. If so, then the right-hand side of Eq. (13.1.1) will have to be modified to reflect such “symmetry” between E and B . To see how magnetic fields can be created by a time-varying electric field, consider a capacitor which is being charged. During the charging ...