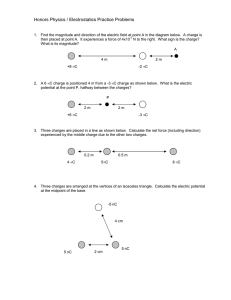
Exam1_Content - Massachusetts Institute of Technology
... a finite line of charge; the field on the axis of a ring of charge; and so on. (2) To be able to recognize and/or draw the electric field line patterns for a small number of discrete charges, for example two point charges of the same or of opposite sign. (3) To be able to apply the principle of supe ...
... a finite line of charge; the field on the axis of a ring of charge; and so on. (2) To be able to recognize and/or draw the electric field line patterns for a small number of discrete charges, for example two point charges of the same or of opposite sign. (3) To be able to apply the principle of supe ...
713 Analyze
... 1. A free electron and a free proton are released in identical electric fields. (i) How do the magnitudes of the electric force exerted on the two particles compare? (a) It is millions of times greater for the electron. (b) It is thousands of times greater for the electron. (c) They are equal. (d) I ...
... 1. A free electron and a free proton are released in identical electric fields. (i) How do the magnitudes of the electric force exerted on the two particles compare? (a) It is millions of times greater for the electron. (b) It is thousands of times greater for the electron. (c) They are equal. (d) I ...
HV Board project - INFN-LNF
... The physical limitations of the practical transformer may be brought together as an equivalent circuit model built around an ideal lossless transformer ...
... The physical limitations of the practical transformer may be brought together as an equivalent circuit model built around an ideal lossless transformer ...
Exam 1 Solutions
... The flux through the bottom face is E ⋅ A = − EA = −40 . The negative sign arises because the normal to the surface is outward (down) and the E field is pointing upward. The total flux through the top and bottom faces is zero, and there is no contribution from the other four faces (normals are perpe ...
... The flux through the bottom face is E ⋅ A = − EA = −40 . The negative sign arises because the normal to the surface is outward (down) and the E field is pointing upward. The total flux through the top and bottom faces is zero, and there is no contribution from the other four faces (normals are perpe ...
• Quantitative rule for computing the magnetic field from any electric
... another right hand rule?! Curl fingers around direction of CURRENT. Thumb points along FIELD! Into page in this case. ...
... another right hand rule?! Curl fingers around direction of CURRENT. Thumb points along FIELD! Into page in this case. ...
document
... flux density, and B the magnetic flux density. Moreover, Jtot = J + Jext , where J is the induced (field dependent) electric-current density, and Jext is the external electric-current densities. In addition to Maxwell’s equations, the compatibility equations have to be satisfied as well. In integrat ...
... flux density, and B the magnetic flux density. Moreover, Jtot = J + Jext , where J is the induced (field dependent) electric-current density, and Jext is the external electric-current densities. In addition to Maxwell’s equations, the compatibility equations have to be satisfied as well. In integrat ...
Homework#1
... particle energy in the equatorial plane: (vgc )Wtot= (vE + vGC) (q+W)=0, and use the fact that since this must be satisfied for arbitrary potentials, including =0, it must be: vGC =c (zW), where c is a constant – then determine the constant. Next show that in the electrostatic potential and W/ ...
... particle energy in the equatorial plane: (vgc )Wtot= (vE + vGC) (q+W)=0, and use the fact that since this must be satisfied for arbitrary potentials, including =0, it must be: vGC =c (zW), where c is a constant – then determine the constant. Next show that in the electrostatic potential and W/ ...
Solenoids
... the coil to become an “electromagnet”. • Air-core solenoids have nothing inside of them. • Iron-core solenoids are filled with iron to intensify the magnetic field. ...
... the coil to become an “electromagnet”. • Air-core solenoids have nothing inside of them. • Iron-core solenoids are filled with iron to intensify the magnetic field. ...
Lecture 17: Ampere`s law
... There is an equal an opposite force exerted by current I2 on I1. The wires thus attract each other. If current I1is reversed, B1 would be in opposite direction. Therefore we find that antiparallel currents repel. ...
... There is an equal an opposite force exerted by current I2 on I1. The wires thus attract each other. If current I1is reversed, B1 would be in opposite direction. Therefore we find that antiparallel currents repel. ...
hw1 - atmo.arizona.edu
... infinitely long and straight, and that the total charge per unit length contained in the envelope of space charge is λo (C/m), derive an expression for the electric field, E(r), everywhere inside and outside the space charge radius. You can assume that the volume charge density (ρo) within R is unif ...
... infinitely long and straight, and that the total charge per unit length contained in the envelope of space charge is λo (C/m), derive an expression for the electric field, E(r), everywhere inside and outside the space charge radius. You can assume that the volume charge density (ρo) within R is unif ...