Shining Light on Modifications of Gravity
... where X = −(∂φ)2 /2, and |B| = −B. The metric (1.1) now defines the geodesics and light cones for the particles of the Standard Model. The first term in this expression is known as the conformal term, and the case A ≡ A(φ) and B ≡ 0 has been much studied. For light, m < (1 mm)−1 , conformally coupl ...
... where X = −(∂φ)2 /2, and |B| = −B. The metric (1.1) now defines the geodesics and light cones for the particles of the Standard Model. The first term in this expression is known as the conformal term, and the case A ≡ A(φ) and B ≡ 0 has been much studied. For light, m < (1 mm)−1 , conformally coupl ...
Renormalization
... difficulties remained. It was widely believed that only a limited class of ‘renormalizable’ theories made physical sense. (The fact that general relativity is not renormalizable in this sense was therefore considered a deep problem.) Also, the renormalization program was viewed by many physicists as ...
... difficulties remained. It was widely believed that only a limited class of ‘renormalizable’ theories made physical sense. (The fact that general relativity is not renormalizable in this sense was therefore considered a deep problem.) Also, the renormalization program was viewed by many physicists as ...
Introduction - the Max Planck Institute for the Physics of Complex
... the symmetric cut and right panels show one of the asymmetric cuts (see above). The blue squares represent numerically obtained data. The assigned edge modes are labeled by green dots while the combinations of those edges are marked by red crosses. The script letters are microscopic identifiers for ...
... the symmetric cut and right panels show one of the asymmetric cuts (see above). The blue squares represent numerically obtained data. The assigned edge modes are labeled by green dots while the combinations of those edges are marked by red crosses. The script letters are microscopic identifiers for ...
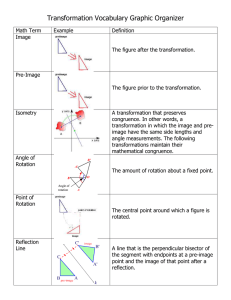
transformations vocabulary review
... A fixed point in the plane about which all points are expanded or contracted. It is the only invariant point under a dilation. A dilation of scalar factor k whose center of dilation is the origin may be written: Dk (x, y) = (kx, ky). If the scale factor, k, is greater than 1, the image is an enlarge ...
... A fixed point in the plane about which all points are expanded or contracted. It is the only invariant point under a dilation. A dilation of scalar factor k whose center of dilation is the origin may be written: Dk (x, y) = (kx, ky). If the scale factor, k, is greater than 1, the image is an enlarge ...
Vincent Gammill
... down when the system is infinitely large, and symmetries can be “broken”. We return to this point in the next Section. Quantum phase transitions, on the other hand, can only be achieved by scaling some parameter (such as electric field) at T = 0, by definition. They are driven by quantum, rather tha ...
... down when the system is infinitely large, and symmetries can be “broken”. We return to this point in the next Section. Quantum phase transitions, on the other hand, can only be achieved by scaling some parameter (such as electric field) at T = 0, by definition. They are driven by quantum, rather tha ...
Symmetries and quantum field theory: an introduction Jean-No¨ el Fuchs
... The mathematical tools needed to describe symmetries are groups and their representations. What is a symmetry? To answer that question precisely, we need to define a few important notions. First, there are transformations. This is a change in our description of a system. I adopt the passive viewpoin ...
... The mathematical tools needed to describe symmetries are groups and their representations. What is a symmetry? To answer that question precisely, we need to define a few important notions. First, there are transformations. This is a change in our description of a system. I adopt the passive viewpoin ...
Bosonic Symmetry Protected Topological States: Theory, Numerics
... Leonard Hofstadter from the Big Bang Theory: There's this farmer, and he has these chickens, but they won't lay any eggs. So, he calls a physicist to help. The physicist then does some calculations, and he says, um, I have a solution, but it only works with spherical chickens in a vacuum! • Topologi ...
... Leonard Hofstadter from the Big Bang Theory: There's this farmer, and he has these chickens, but they won't lay any eggs. So, he calls a physicist to help. The physicist then does some calculations, and he says, um, I have a solution, but it only works with spherical chickens in a vacuum! • Topologi ...
Why dynamics?
... If disorder does not destroy QCP via Harris criterion, one can study dynamics across disordered QCP. This might lead to different scaling laws for defect density and residual energy originating from disorder averaging. Study of Kitaev model by Hikichi, Suzuki and KS ( PRB 2010). Presence of external ...
... If disorder does not destroy QCP via Harris criterion, one can study dynamics across disordered QCP. This might lead to different scaling laws for defect density and residual energy originating from disorder averaging. Study of Kitaev model by Hikichi, Suzuki and KS ( PRB 2010). Presence of external ...
Synthetic quantum field theory
... David Hilbert, ICM, Paris 1900: Mathematical Problem 6: To treat [...] by means of axioms, those physical sciences in which mathematics plays an important part try first by a small number of axioms to include as large a class as possible of physical phenomena, and then by adjoining new axioms to arr ...
... David Hilbert, ICM, Paris 1900: Mathematical Problem 6: To treat [...] by means of axioms, those physical sciences in which mathematics plays an important part try first by a small number of axioms to include as large a class as possible of physical phenomena, and then by adjoining new axioms to arr ...
Particle Physics and the LHC
... The Naturalness Argument • If there are very large/small parameters in a quantum theory, there must be a good reason why they are so small…. • In general, there will be large quantum corrections to such parameters in higher orders of perturbation theory, in terms of other parameters which are not s ...
... The Naturalness Argument • If there are very large/small parameters in a quantum theory, there must be a good reason why they are so small…. • In general, there will be large quantum corrections to such parameters in higher orders of perturbation theory, in terms of other parameters which are not s ...
The Beauty of Mathematics
... For those who are mathematically inclined, there is often a definite aesthetic aspect to much of mathematics. Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty in a simple and elegant proof and ...
... For those who are mathematically inclined, there is often a definite aesthetic aspect to much of mathematics. Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty in a simple and elegant proof and ...
ACTION AT A DISTANCE AND COSMOLOGY: A Historical
... Also, according to the Lorentz force equation, R (b) is the force arising from all other particles in the universe experienced by the particle B. This is nothing but the radiative reaction to the motion of b as obtained earlier by Dirac (1938) on empirical grounds. Dirac had shown that the Lorentz f ...
... Also, according to the Lorentz force equation, R (b) is the force arising from all other particles in the universe experienced by the particle B. This is nothing but the radiative reaction to the motion of b as obtained earlier by Dirac (1938) on empirical grounds. Dirac had shown that the Lorentz f ...
Unparticle_Dark_Matter_(GUT07)
... Introduction • Beyond the SM (for model buildings in this LHC era): Are there totally unexpected phenomena which has not yet discovered so far? What would be expected to happen at LHC that might be originated from some unknown models, not only SUSY or extra dimensional models, etc.? This is basical ...
... Introduction • Beyond the SM (for model buildings in this LHC era): Are there totally unexpected phenomena which has not yet discovered so far? What would be expected to happen at LHC that might be originated from some unknown models, not only SUSY or extra dimensional models, etc.? This is basical ...
Open-Closed String Duality in Field Theory? - damtp
... I therefore claim that the relative dynamics of two domain walls is governed by a d = 2+1, N = 2 supersymmetric U(1) gauge theory coupled to a single chiral multiplet. However, there is a subtlety. Integrating out a charged chiral multiplet in d = 2 + 1 dimensions induces a Chern-Simons coupling. In ...
... I therefore claim that the relative dynamics of two domain walls is governed by a d = 2+1, N = 2 supersymmetric U(1) gauge theory coupled to a single chiral multiplet. However, there is a subtlety. Integrating out a charged chiral multiplet in d = 2 + 1 dimensions induces a Chern-Simons coupling. In ...
Bose-Einstein Condensation and Free DKP field
... atomic traps [7] many atoms condense to the ground state of the trap, in quantum field theory BEC is commonly related to spontaneous symmetry breaking [8, 9, 10]. In quantum field theory BEC the complex scalar field was and is used for studying the thermodynamical properties of physical systems comp ...
... atomic traps [7] many atoms condense to the ground state of the trap, in quantum field theory BEC is commonly related to spontaneous symmetry breaking [8, 9, 10]. In quantum field theory BEC the complex scalar field was and is used for studying the thermodynamical properties of physical systems comp ...
Scale invariance

In physics, mathematics, statistics, and economics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor. The technical term for this transformation is a dilatation (also known as dilation), and the dilatations can also form part of a larger conformal symmetry.In mathematics, scale invariance usually refers to an invariance of individual functions or curves. A closely related concept is self-similarity, where a function or curve is invariant under a discrete subset of the dilatations. It is also possible for the probability distributions of random processes to display this kind of scale invariance or self-similarity.In classical field theory, scale invariance most commonly applies to the invariance of a whole theory under dilatations. Such theories typically describe classical physical processes with no characteristic length scale.In quantum field theory, scale invariance has an interpretation in terms of particle physics. In a scale-invariant theory, the strength of particle interactions does not depend on the energy of the particles involved.In statistical mechanics, scale invariance is a feature of phase transitions. The key observation is that near a phase transition or critical point, fluctuations occur at all length scales, and thus one should look for an explicitly scale-invariant theory to describe the phenomena. Such theories are scale-invariant statistical field theories, and are formally very similar to scale-invariant quantum field theories.Universality is the observation that widely different microscopic systems can display the same behaviour at a phase transition. Thus phase transitions in many different systems may be described by the same underlying scale-invariant theory.In general, dimensionless quantities are scale invariant. The analogous concept in statistics are standardized moments, which are scale invariant statistics of a variable, while the unstandardized moments are not.




![arXiv:1203.2158v1 [hep-th] 9 Mar 2012 The “tetrad only” theory](http://s1.studyres.com/store/data/016613184_1-9fc43c0ba152dfbab9c386708b4475ee-300x300.png)