Relational Predicate Logic
... One way better to understand sentences which include overlapping quantifiers is to become familiar with the expansions of such multiply quantified sentences. ...
... One way better to understand sentences which include overlapping quantifiers is to become familiar with the expansions of such multiply quantified sentences. ...
Ch1 - COW :: Ceng
... Semantics: meaning for the language Reasoning: Proof theory Model theory ...
... Semantics: meaning for the language Reasoning: Proof theory Model theory ...
(formal) logic? - Departamento de Informática
... intuitionistic logic, but the task is very difficult, so mathematicians use methods of classical logic (as proofs by contradiction). However the philosophy behind intuitionistic logic is appealing for a computer scientist. For an intuitionist, a mathematical object (such as the solution of an equation ...
... intuitionistic logic, but the task is very difficult, so mathematicians use methods of classical logic (as proofs by contradiction). However the philosophy behind intuitionistic logic is appealing for a computer scientist. For an intuitionist, a mathematical object (such as the solution of an equation ...
pdf
... Where logic has space But in it we only outfool2 The students do enter the class Afraid of notation and maths At the end come out they Feeling just the same way And hating the logical paths ...
... Where logic has space But in it we only outfool2 The students do enter the class Afraid of notation and maths At the end come out they Feeling just the same way And hating the logical paths ...
Jean Van Heijenoort`s View of Modern Logic
... the proposition into subject and predicate had been replaced by its analysis into function and argument(s). A preliminary accomplishment was the propositional calculus, with a truth-functional definition of the connectives, including the conditional. Of cardinal importance was the realization that, ...
... the proposition into subject and predicate had been replaced by its analysis into function and argument(s). A preliminary accomplishment was the propositional calculus, with a truth-functional definition of the connectives, including the conditional. Of cardinal importance was the realization that, ...
first order logic
... We have not defined formally what is a set, and will do so later in the course. For now, it is enough for our discussion to recall some well-known examples. Z: the set of all integers Z+: the set of all positive integers Z-: the set of all negative integers R: the set of all real numbers Q: the set ...
... We have not defined formally what is a set, and will do so later in the course. For now, it is enough for our discussion to recall some well-known examples. Z: the set of all integers Z+: the set of all positive integers Z-: the set of all negative integers R: the set of all real numbers Q: the set ...
Epistemological Vs - Birkbeck, University of London
... But why all this creative reconstruction, all this make believe? The stimulation of his sensory receptors is all the evidence anybody has had to go on, ultimately, in arriving at his picture of the world. Why not just see how this construction really proceeds? Why not settle for psychology! (Quine ( ...
... But why all this creative reconstruction, all this make believe? The stimulation of his sensory receptors is all the evidence anybody has had to go on, ultimately, in arriving at his picture of the world. Why not just see how this construction really proceeds? Why not settle for psychology! (Quine ( ...
Lecture Notes in Computer Science
... Several recent extensions of definite Horn clause programming, especially those with a proof-theoretic background, have much in common. One common thread is a new emphasis on hypothetical reasoning, which is typically inspired by Gentzen-style sequent or natural deduction systems. This is not only o ...
... Several recent extensions of definite Horn clause programming, especially those with a proof-theoretic background, have much in common. One common thread is a new emphasis on hypothetical reasoning, which is typically inspired by Gentzen-style sequent or natural deduction systems. This is not only o ...
IS IT EASY TO LEARN THE LOGIC
... the calculations rather than applications of the knowledge we use in practical life, so, for a student of general logic , modus ponens reasoning is not apprehensive, because they break down its semantic context to be applied mechanically. Equally difficult turns out equivalences referred to with tru ...
... the calculations rather than applications of the knowledge we use in practical life, so, for a student of general logic , modus ponens reasoning is not apprehensive, because they break down its semantic context to be applied mechanically. Equally difficult turns out equivalences referred to with tru ...
Lecture 11 Artificial Intelligence Predicate Logic
... appealing because you can derive new knowledge from old mathematical deduction. • In this formalism you can conclude that a new statement is true if by proving that it follows from the statement that are already known. • It provides a way of deducing new statements from old ones. ...
... appealing because you can derive new knowledge from old mathematical deduction. • In this formalism you can conclude that a new statement is true if by proving that it follows from the statement that are already known. • It provides a way of deducing new statements from old ones. ...
Quine on "Alternative Logics"
... are preserved in translation by matching observable correlations th at hold for a foreign speech community’s dispositions to verdictive behavior with correlations t ha t hold for our own dispositions. In Word and Object Quine offers three semantic criteria that allegedly fully determine the meaning ...
... are preserved in translation by matching observable correlations th at hold for a foreign speech community’s dispositions to verdictive behavior with correlations t ha t hold for our own dispositions. In Word and Object Quine offers three semantic criteria that allegedly fully determine the meaning ...
quine`s argument from despair
... conceptual side of epistemology, Locke, Berkeley, and Hume were unable to indicate how our complex ideas about the world can be constructed out of indubitable simple ones; defining even the very notion of an enduring physical body turned out to be problematic (1946, 57-77). Still, their problems wer ...
... conceptual side of epistemology, Locke, Berkeley, and Hume were unable to indicate how our complex ideas about the world can be constructed out of indubitable simple ones; defining even the very notion of an enduring physical body turned out to be problematic (1946, 57-77). Still, their problems wer ...
Lecture 16 Notes
... results we cited in Lecture 15 that show i FOL to be incomplete with respect to the intuitionistic version of classical Tarski semantics. We briefly touched on this semantics in Lecture 14, citing Troelstra and van Dalen for the result that i FOL is incomplete for this “standard intuitionistic seman ...
... results we cited in Lecture 15 that show i FOL to be incomplete with respect to the intuitionistic version of classical Tarski semantics. We briefly touched on this semantics in Lecture 14, citing Troelstra and van Dalen for the result that i FOL is incomplete for this “standard intuitionistic seman ...
Knowledge Representation
... • There is a precise meaning to expressions in predicate logic. • Like in propositional logic, it is all about determining whether something is true or false. • X P(X) means that P(X) must be true for every object X in the domain of interest. • X P(X) means that P(X) must be true for at least on ...
... • There is a precise meaning to expressions in predicate logic. • Like in propositional logic, it is all about determining whether something is true or false. • X P(X) means that P(X) must be true for every object X in the domain of interest. • X P(X) means that P(X) must be true for at least on ...
Negative translation - Homepages of UvA/FNWI staff
... obtained from intuitionistic logic by adding an additional axiom (for instance, the Law of Excluded Middle ϕ ∨ ¬ϕ). However, the opposite point of view makes sense as well: one could also think of intuitionistic logic as an extension of classical logic. The reason for this is that there is a faithfu ...
... obtained from intuitionistic logic by adding an additional axiom (for instance, the Law of Excluded Middle ϕ ∨ ¬ϕ). However, the opposite point of view makes sense as well: one could also think of intuitionistic logic as an extension of classical logic. The reason for this is that there is a faithfu ...
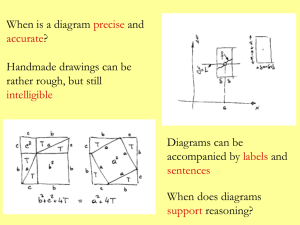
Diagrams in logic and mathematics - CFCUL
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
What is Logic?
... “If There exists an x for which P holds, then it is not true that for all x P does not hold”. ...
... “If There exists an x for which P holds, then it is not true that for all x P does not hold”. ...
Chapter 7 Propositional and Predicate Logic
... It is Raining and it is Thursday: R Λ T R means “It is Raining”, T means “it is Thursday”. ...
... It is Raining and it is Thursday: R Λ T R means “It is Raining”, T means “it is Thursday”. ...
PHIL 160: Introduction to Philosophy of Science
... What is the kind of evidence that supports scientific hypotheses and/or theories? How strong is that evidence? Suppose a theory includes objects (such as quarks) or historical events/processes (such as geological or evolutionary events/processes) that are not directly observable? What kind of eviden ...
... What is the kind of evidence that supports scientific hypotheses and/or theories? How strong is that evidence? Suppose a theory includes objects (such as quarks) or historical events/processes (such as geological or evolutionary events/processes) that are not directly observable? What kind of eviden ...
Quining Naturalism
... predicates—say, the terms we use in talking about medium sized objects, or in talking about numbers. Carnap thought that adopting such a framework, or way of talking, typically brings with it ontological methods and questions. These are ‘internal’ questions, questions that arise within the framework ...
... predicates—say, the terms we use in talking about medium sized objects, or in talking about numbers. Carnap thought that adopting such a framework, or way of talking, typically brings with it ontological methods and questions. These are ‘internal’ questions, questions that arise within the framework ...
Kinds of Things—Towards a Bestiary of the
... there sakes? Are there miles? He used these homely examples to loosen up his readers for his theory-driven proposals, his quest for a ‘desert landscape’ clean-shaven by Occam’s Razor, a minimalist ontology for science (and for everything worth talking and thinking about—he was Carnap’s student, afte ...
... there sakes? Are there miles? He used these homely examples to loosen up his readers for his theory-driven proposals, his quest for a ‘desert landscape’ clean-shaven by Occam’s Razor, a minimalist ontology for science (and for everything worth talking and thinking about—he was Carnap’s student, afte ...
Natural Deduction Calculus for Quantified Propositional Linear
... While the propositional quantification does not add any expressiveness to the classical logic QPTL is more expressive than PLTL presenting the same potential of expressiveness as linear-time µ-calculus (linear-time propositional temporal fixpoint logic) [Kaivola (1997)], ETL (propositional linear-ti ...
... While the propositional quantification does not add any expressiveness to the classical logic QPTL is more expressive than PLTL presenting the same potential of expressiveness as linear-time µ-calculus (linear-time propositional temporal fixpoint logic) [Kaivola (1997)], ETL (propositional linear-ti ...
Section 6.1 How Do We Reason? We make arguments, where an
... followed by a single statement, called the conclusion. The hope is that we make valid arguments, where an argument is valid if the truth of the premises implies the truth of the conclusion. We can use rules of logic to make valid arguments. The most common rule of logic is modus ponens (mode that af ...
... followed by a single statement, called the conclusion. The hope is that we make valid arguments, where an argument is valid if the truth of the premises implies the truth of the conclusion. We can use rules of logic to make valid arguments. The most common rule of logic is modus ponens (mode that af ...
Normative Ethics, Normative Epistemology, and Quine`s Holism
... our moral standards themselves. Science, thanks to its links with observation, retains some title to a correspondence theory of truth; but a coherence theory is evidently the lot of ethics\".} Quine has also maintained that when empiricism reached its fifth and most recent milestone it assimilated e ...
... our moral standards themselves. Science, thanks to its links with observation, retains some title to a correspondence theory of truth; but a coherence theory is evidently the lot of ethics\".} Quine has also maintained that when empiricism reached its fifth and most recent milestone it assimilated e ...
Normalised and Cut-free Logic of Proofs
... From a Gentzen-style point of view, we can formulate two similar sequent calculi for the two systems Lp and Ilp, respectively (see Artemov [2002]). Although simple and cut-free, these sequent calculi fail to satisfy certain properties that are standardly required from a “good" sequent calculus (in P ...
... From a Gentzen-style point of view, we can formulate two similar sequent calculi for the two systems Lp and Ilp, respectively (see Artemov [2002]). Although simple and cut-free, these sequent calculi fail to satisfy certain properties that are standardly required from a “good" sequent calculus (in P ...
Willard Van Orman Quine

Willard Van Orman Quine (/kwaɪn/; June 25, 1908 – December 25, 2000) (known to intimates as ""Van"") was an American philosopher and logician in the analytic tradition, recognized as ""one of the most influential philosophers of the twentieth century."" From 1930 until his death 70 years later, Quine was continually affiliated with Harvard University in one way or another, first as a student, then as a professor of philosophy and a teacher of logic and set theory, and finally as a professor emeritus who published or revised several books in retirement. He filled the Edgar Pierce Chair of Philosophy at Harvard from 1956 to 1978. A recent poll conducted among analytic philosophers named Quine as the fifth most important philosopher of the past two centuries. He won the first Schock Prize in Logic and Philosophy in 1993 for ""his systematical and penetrating discussions of how learning of language and communication are based on socially available evidence and of the consequences of this for theories on knowledge and linguistic meaning."" In 1996 he was awarded the Kyoto Prize in Arts and Philosophy for his ""outstanding contributions to the progress of philosophy in the 20th century by proposing numerous theories based on keen insights in logic, epistemology, philosophy of science and philosophy of language.""Quine falls squarely into the analytic philosophy tradition while also being the main proponent of the view that philosophy is not conceptual analysis but the abstract branch of the empirical sciences. His major writings include ""Two Dogmas of Empiricism"" (1951), which attacked the distinction between analytic and synthetic propositions and advocated a form of semantic holism, and Word and Object (1960), which further developed these positions and introduced Quine's famous indeterminacy of translation thesis, advocating a behaviorist theory of meaning. He also developed an influential naturalized epistemology that tried to provide ""an improved scientific explanation of how we have developed elaborate scientific theories on the basis of meager sensory input."" He is also important in philosophy of science for his ""systematic attempt to understand science from within the resources of science itself"" and for his conception of philosophy as continuous with science. This led to his famous quip that ""philosophy of science is philosophy enough."" In philosophy of mathematics, he and his Harvard colleague Hilary Putnam developed the ""Quine–Putnam indispensability thesis,"" an argument for the reality of mathematical entities.