Document
... Deductive Argumentation. Its procedure is best learned from Book I of Euclid’s Elements.” (Essential Peirce, p. 441) “Kant is entirely right in saying that, in drawing those consequences, the mathematician uses what, in geometry, is called a ‘construction’, or in general a diagram, or visual array o ...
... Deductive Argumentation. Its procedure is best learned from Book I of Euclid’s Elements.” (Essential Peirce, p. 441) “Kant is entirely right in saying that, in drawing those consequences, the mathematician uses what, in geometry, is called a ‘construction’, or in general a diagram, or visual array o ...
Bound and Free Variables Theorems and Proofs
... and one inference rule: Modus Ponens: • From A ⇒ B and A infer B Ax1 and Ax2 are axioms schemes: • each one encodes an infinite set of axioms (obtained by plugging in arbitrary formulas for A, B, C A proof is a sequence of formulas A1, A2, A3, . . . such that each Ai is either 1. An instance of Ax1 ...
... and one inference rule: Modus Ponens: • From A ⇒ B and A infer B Ax1 and Ax2 are axioms schemes: • each one encodes an infinite set of axioms (obtained by plugging in arbitrary formulas for A, B, C A proof is a sequence of formulas A1, A2, A3, . . . such that each Ai is either 1. An instance of Ax1 ...
Predicate logic
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
Predicate Logic
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
PHILOSOPHY 326 / MATHEMATICS 307 SYMBOLIC LOGIC This
... 114, Introduction to Symbolic Logic, is a prerequisite for Philosophy 326 (or Mathematics 307). It is assumed that all students will have a thorough grasp of the fundamentals of the two-valued logic of propositions – including the fundamental vocabulary of formal deductive logic, the basic two-value ...
... 114, Introduction to Symbolic Logic, is a prerequisite for Philosophy 326 (or Mathematics 307). It is assumed that all students will have a thorough grasp of the fundamentals of the two-valued logic of propositions – including the fundamental vocabulary of formal deductive logic, the basic two-value ...
03_Artificial_Intelligence-PredicateLogic
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
ppt
... and only if it is true under all possible interpretations in all possible domains. • For example: If Today_Is_Tuesday Then We_Have_Class ...
... and only if it is true under all possible interpretations in all possible domains. • For example: If Today_Is_Tuesday Then We_Have_Class ...
03_Artificial_Intelligence-PredicateLogic
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
Proof Theory in Type Theory
... Introduction The negative translation provides a general way to make constructive sense of some non effective reasoning. However this method has some limitations. It does not work in presence of the axiom of description/choice. In this note, we analyse the interaction of classical logic with general ...
... Introduction The negative translation provides a general way to make constructive sense of some non effective reasoning. However this method has some limitations. It does not work in presence of the axiom of description/choice. In this note, we analyse the interaction of classical logic with general ...
Chapter 1: The Foundations: Logic and Proofs
... • We use letters to denote propositional variables (or statement variables). • T: the value of a proposition is true. • F: the value of a proposition is false. • The area of logic that deals with propositions is called the propositional calculus or propositional logic. ...
... • We use letters to denote propositional variables (or statement variables). • T: the value of a proposition is true. • F: the value of a proposition is false. • The area of logic that deals with propositions is called the propositional calculus or propositional logic. ...
Predicate logic - Teaching-WIKI
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
Predicate logic
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
... sentences would just be a represented by some proposition, say P, Q and R. What relationship is there between these propositions? We can say P /\ Q → R Then, given P /\ Q, we could indeed conclude R. But now, suppose we were told Pat is standing in the rain. ...
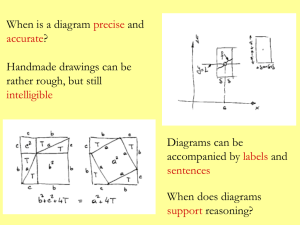
Diagrams in logic and mathematics - CFCUL
... Barwise - Etchemendy (1996), ‘Visual Information and Valid Reasoning’, in Allwein Barwise (eds.) (1996), Logical Reasoning with Diagrams, 3-25. Brown (1999), Philosophy of Mathematics: an introduction to the world of proofs and pictures. Giaquinto (2007), Visual Thinking in Mathematics. Polya (1945) ...
... Barwise - Etchemendy (1996), ‘Visual Information and Valid Reasoning’, in Allwein Barwise (eds.) (1996), Logical Reasoning with Diagrams, 3-25. Brown (1999), Philosophy of Mathematics: an introduction to the world of proofs and pictures. Giaquinto (2007), Visual Thinking in Mathematics. Polya (1945) ...
Sequent calculus - Wikipedia, the free encyclopedia
... Consider, for example, the rule (∧L 1). It says that, whenever one can prove that Δ can be concluded from some sequence of formulae that contain A, then one can also conclude Δ from the (stronger) assumption, that A∧B holds. Likewise, the rule (¬R) states that, if Γ and A suffice to conclude Δ, then ...
... Consider, for example, the rule (∧L 1). It says that, whenever one can prove that Δ can be concluded from some sequence of formulae that contain A, then one can also conclude Δ from the (stronger) assumption, that A∧B holds. Likewise, the rule (¬R) states that, if Γ and A suffice to conclude Δ, then ...
CLASSICAL LOGIC and FUZZY LOGIC
... described by the following collection of elements, X = {1, 2, 3, 4} and Y = {1, 2, 3, 4, 5, 6}. Suppose X is a universe of normalized temperatures and Y is a universe of normalized pressures. Define crisp set A on universe X and crisp set B on universe Y as follows: A = {2, 3} and B = {3, 4}. The de ...
... described by the following collection of elements, X = {1, 2, 3, 4} and Y = {1, 2, 3, 4, 5, 6}. Suppose X is a universe of normalized temperatures and Y is a universe of normalized pressures. Define crisp set A on universe X and crisp set B on universe Y as follows: A = {2, 3} and B = {3, 4}. The de ...
Comments on predicative logic
... apart from the natural conversions associated with the connectives (removal of local peaks), must be made available in order to have a decent theory of normalization of derivations. Girard et al. point out that there is currently no alternative to the bad rules, although they hasten to say that the ...
... apart from the natural conversions associated with the connectives (removal of local peaks), must be made available in order to have a decent theory of normalization of derivations. Girard et al. point out that there is currently no alternative to the bad rules, although they hasten to say that the ...
Propositional Logic and Methods of Inference
... Terms such as Pi, must be literals, which mean that they contain no logical connectives such as the conditional and biconditional, or quantifiers ...
... Terms such as Pi, must be literals, which mean that they contain no logical connectives such as the conditional and biconditional, or quantifiers ...
Inquiry
An inquiry is any process that has the aim of augmenting knowledge, resolving doubt, or solving a problem. A theory of inquiry is an account of the various types of inquiry and a treatment of the ways that each type of inquiry achieves its aim.