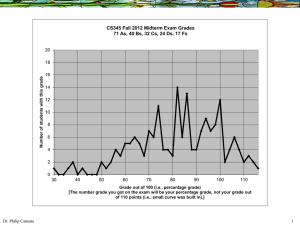
article - British Academy
... principle’: if one knows something, one knows that one knows it. He does not accept the principle, and nor do I; but whether one accepts it or not, the question arises how it should be formulated. Consider For all p, if t knows that p, then t knows that t knows that p. Substituting ‘I’ for t gives, ...
... principle’: if one knows something, one knows that one knows it. He does not accept the principle, and nor do I; but whether one accepts it or not, the question arises how it should be formulated. Consider For all p, if t knows that p, then t knows that t knows that p. Substituting ‘I’ for t gives, ...
Three Solutions to the Knower Paradox
... enumerable and contains Q, Robinson Arithmetic (as we will see in a moment, K0 has to contain Q, otherwise James could never be me, as Anderson wants). Hence James knows by a syntactic notion of proof, and so, for what we have just said, he doesn’t know the Gödel sentence G: nobody, who knows by thi ...
... enumerable and contains Q, Robinson Arithmetic (as we will see in a moment, K0 has to contain Q, otherwise James could never be me, as Anderson wants). Hence James knows by a syntactic notion of proof, and so, for what we have just said, he doesn’t know the Gödel sentence G: nobody, who knows by thi ...
Predicate Logic for Software Engineering
... From a drop of water a logician could infer the possibility of an Atlantic or a Niagara Sri without having seen or heard of one or the other. * Sir Arthur Conan Doyle ...
... From a drop of water a logician could infer the possibility of an Atlantic or a Niagara Sri without having seen or heard of one or the other. * Sir Arthur Conan Doyle ...
Prolog 1 - Department of Computer Science
... soundness refers to logical systems, which means that if some formula can be proven in a system, then it is true in the relevant model/structure (if A is a theorem, it is true). This is the converse of completeness. Unsoundness usually violates our innate notion of Excluded Middle – but so do so man ...
... soundness refers to logical systems, which means that if some formula can be proven in a system, then it is true in the relevant model/structure (if A is a theorem, it is true). This is the converse of completeness. Unsoundness usually violates our innate notion of Excluded Middle – but so do so man ...
An Axiomatization of G'3
... or equal to a logic Y if X ⊆ Y , similarly we say that X is stronger than or equal to Y if Y ⊆ X. Hilbert Style Proof Systems. There are many different approaches that have been used to specify the meaning of logic formulas or, in other words, to define logics. In Hilbert style proof systems, also k ...
... or equal to a logic Y if X ⊆ Y , similarly we say that X is stronger than or equal to Y if Y ⊆ X. Hilbert Style Proof Systems. There are many different approaches that have been used to specify the meaning of logic formulas or, in other words, to define logics. In Hilbert style proof systems, also k ...
1992-Ideal Introspective Belief
... derivable from the premises alone. For example, consider the premise set {lLp > q,p V q}. We would like since there is no reasonable way of to conclude ‘Lp, coming to believe p. But an inference rule that would allow us to conclude 1Lp would have to take into account all possible derivations, includ ...
... derivable from the premises alone. For example, consider the premise set {lLp > q,p V q}. We would like since there is no reasonable way of to conclude ‘Lp, coming to believe p. But an inference rule that would allow us to conclude 1Lp would have to take into account all possible derivations, includ ...
Chapter 5 Predicate Logic
... f (H) = {hm, mi, hm, ni, hm, Ni, hn, ni, hn, Ni, hN, Ni}. We can use this latter interpretation of H to treat another predicate logic formula: (∀x)H(x, x). Here there is still only one quantifier and no connectives, but there is more than one quantified variable. The interpretation is that both argu ...
... f (H) = {hm, mi, hm, ni, hm, Ni, hn, ni, hn, Ni, hN, Ni}. We can use this latter interpretation of H to treat another predicate logic formula: (∀x)H(x, x). Here there is still only one quantifier and no connectives, but there is more than one quantified variable. The interpretation is that both argu ...
Hoare Logic, Weakest Liberal Preconditions
... Proof. We prove this theorem by directly considering the definition of triples, in terms of operational semantics. It would also be possible to prove the validity of the triple using Hoare logic rules, but that would need some auxiliary results. The proof is performed by induction on the structure o ...
... Proof. We prove this theorem by directly considering the definition of triples, in terms of operational semantics. It would also be possible to prove the validity of the triple using Hoare logic rules, but that would need some auxiliary results. The proof is performed by induction on the structure o ...
Propositional Logic
... § If P is False, regardless of Q, P ⇒ Q is True § No causality needed: “5 is odd implies the Sun is a star” is True ...
... § If P is False, regardless of Q, P ⇒ Q is True § No causality needed: “5 is odd implies the Sun is a star” is True ...
Gödel`s ontological argument: a reply to Oppy
... (i.e., possibly instantiated). This is where Leibniz’s attempt to prove God’s possibility is most questionable. How can we assume that the set of all positive, or in Leibniz’s case, simple, properties is consistent? This is a question which Gödel’s argument doesn’t answer any better than Leibniz’s. ...
... (i.e., possibly instantiated). This is where Leibniz’s attempt to prove God’s possibility is most questionable. How can we assume that the set of all positive, or in Leibniz’s case, simple, properties is consistent? This is a question which Gödel’s argument doesn’t answer any better than Leibniz’s. ...
Lecture 2: Language of logic, truth tables
... • On a mystical island, there are two kinds of people: knights and knaves. Knights always tell the truth. Knaves always lie. • Puzzle 1: You meet two people on the island, Arnold and Bob. Arnold says “Either I am a knave, or Bob is a knight”. Is Arnold a knight or a knave? What about Bob? ...
... • On a mystical island, there are two kinds of people: knights and knaves. Knights always tell the truth. Knaves always lie. • Puzzle 1: You meet two people on the island, Arnold and Bob. Arnold says “Either I am a knave, or Bob is a knight”. Is Arnold a knight or a knave? What about Bob? ...
Document
... two-valued logic – every sentence is either true or false some sentences are minimal – no proper part which is also a sentence others – can be taken apart into smaller parts we can build larger sentences from smaller ones by using connectives ...
... two-valued logic – every sentence is either true or false some sentences are minimal – no proper part which is also a sentence others – can be taken apart into smaller parts we can build larger sentences from smaller ones by using connectives ...
propositions and connectives propositions and connectives
... two-valued logic – every sentence is either true or false some sentences are minimal – no proper part which is also a sentence others – can be taken apart into smaller parts we can build larger sentences from smaller ones by using connectives ...
... two-valued logic – every sentence is either true or false some sentences are minimal – no proper part which is also a sentence others – can be taken apart into smaller parts we can build larger sentences from smaller ones by using connectives ...
x - Stanford University
... arguments, but each function has a fixed arity. Functions evaluate to objects, not propositions. There is no syntactic way to distinguish functions and predicates; you'll have to look at how they're used. ...
... arguments, but each function has a fixed arity. Functions evaluate to objects, not propositions. There is no syntactic way to distinguish functions and predicates; you'll have to look at how they're used. ...
Classical Propositional Logic
... DPLL and the refined CDCL algorithm are the practically best methods for PL The resolution calculus (Robinson 1969) has been introduced as a basis for automated theorem proving in first-order logic. We will see it in detail in the first-order logic part of this lecture Refined versions are still the ...
... DPLL and the refined CDCL algorithm are the practically best methods for PL The resolution calculus (Robinson 1969) has been introduced as a basis for automated theorem proving in first-order logic. We will see it in detail in the first-order logic part of this lecture Refined versions are still the ...
IM_FA16-03-PredicateLogic
... But truth tables don’t suffice for PL, we need interpretations. An interpretation is a) A non-empty collection of objects (the domain) b) An assignment of each object to (at least one) name. c) A list of predicates. d) An assignment to each n-place predicate of a set of sequences of n objects of whi ...
... But truth tables don’t suffice for PL, we need interpretations. An interpretation is a) A non-empty collection of objects (the domain) b) An assignment of each object to (at least one) name. c) A list of predicates. d) An assignment to each n-place predicate of a set of sequences of n objects of whi ...
Day00a-Induction-proofs - Rose
... induction? To show that p(n) is true for all n n0 : – Step 0: Believe in the "magic." • You will show that it's not really magic at all. But you have to believe. • If, when you are in the middle of an induction proof, you begin to doubt whether the principle of mathematical induction itself is tru ...
... induction? To show that p(n) is true for all n n0 : – Step 0: Believe in the "magic." • You will show that it's not really magic at all. But you have to believe. • If, when you are in the middle of an induction proof, you begin to doubt whether the principle of mathematical induction itself is tru ...
Predicate Logic - Teaching-WIKI
... Anyone standing in the rain will get wet. and then use this knowledge. For example, suppose we also learn that Jan is standing in the rain. • We'd like to conclude that Jan will get wet. But each of these sentences would just be a represented by some proposition, say P, Q and R. What relationship is ...
... Anyone standing in the rain will get wet. and then use this knowledge. For example, suppose we also learn that Jan is standing in the rain. • We'd like to conclude that Jan will get wet. But each of these sentences would just be a represented by some proposition, say P, Q and R. What relationship is ...
A Nonstandard Approach to the. Logical Omniscience Problem
... serve only as epistemic alternatives; although an agent may be muddled and may consider a nonstandard world possible, we (the logicians who get to examine the situation from t h e outside) know that the "real world" must obey the laws of standard logic. If we consider validity and logical implicatio ...
... serve only as epistemic alternatives; although an agent may be muddled and may consider a nonstandard world possible, we (the logicians who get to examine the situation from t h e outside) know that the "real world" must obey the laws of standard logic. If we consider validity and logical implicatio ...
CHAPTER 1 The Foundations: Logic and Proof, Sets, and Functions
... to content (does each statement follow logically? are you making any fallacious arguments? are you leaving out any cases or using hidden assumptions?) and to style. There are certain conventions in mathematical proofs, and you need to follow them. For example, you must use complete sentences and say ...
... to content (does each statement follow logically? are you making any fallacious arguments? are you leaving out any cases or using hidden assumptions?) and to style. There are certain conventions in mathematical proofs, and you need to follow them. For example, you must use complete sentences and say ...
Language, Proof and Logic
... satisfying S(x), as long as the name is not one that is already in use. We may then assume S(c) and use it in our proof. This is the rule known as existential instantiation or existential elimination. Generally, when existential instantiation is used in a mathematical proof, this will be marked by a ...
... satisfying S(x), as long as the name is not one that is already in use. We may then assume S(c) and use it in our proof. This is the rule known as existential instantiation or existential elimination. Generally, when existential instantiation is used in a mathematical proof, this will be marked by a ...
Chapter 2 Propositional Logic
... and we get another wff. (The resulting wff is often called a “conditional”, whose “antecedent” is the wff before the → and whose “consequent” is the wff after the →.) For example, since we know that Q is a wff (clause i)), and that ∼P is a wff (we just showed this a moment ago), we know that (Q→∼P ) ...
... and we get another wff. (The resulting wff is often called a “conditional”, whose “antecedent” is the wff before the → and whose “consequent” is the wff after the →.) For example, since we know that Q is a wff (clause i)), and that ∼P is a wff (we just showed this a moment ago), we know that (Q→∼P ) ...
On the futility of criticizing the neoclassical maximization hypothesis
... Tautologies are statements which are true by virtue of their logical form alone – that is, one cannot even conceive of how they could ever be false. For example, the statement ‘I am here or I am not here’ is true regardless of the meaning of the non-logical words ‘I’ or ‘here’. There is no conceivab ...
... Tautologies are statements which are true by virtue of their logical form alone – that is, one cannot even conceive of how they could ever be false. For example, the statement ‘I am here or I am not here’ is true regardless of the meaning of the non-logical words ‘I’ or ‘here’. There is no conceivab ...