Vector Calculus
... • Polynominal functions f are continuous at every real number c because limx → c, f(x) = f(c). • Rational functions are continuous at every point of their domains. They have points of discontinuity at the zeros of their denominators. • The absolute value function y = |x| is continuous at every real ...
... • Polynominal functions f are continuous at every real number c because limx → c, f(x) = f(c). • Rational functions are continuous at every point of their domains. They have points of discontinuity at the zeros of their denominators. • The absolute value function y = |x| is continuous at every real ...
Chapter 12 Applications of Series
... Chapter 12 Applications of Series The preceding chapter developed several tests for determining the convergence or divergence of infinite series. This √ chapter applies infinite series to approximate functions such as ex and sin( x), evaluate integrals, and calculate limits of the indeterminate form ...
... Chapter 12 Applications of Series The preceding chapter developed several tests for determining the convergence or divergence of infinite series. This √ chapter applies infinite series to approximate functions such as ex and sin( x), evaluate integrals, and calculate limits of the indeterminate form ...
Sets and Functions
... one of the seven basic assumptions out of which calculus flows. The statements that we assume true (in order to form a starting point for logical deductions) are called axioms. My dictionary 1 defines an axiom to be a “proposition regarded as a self-evident truth”, and this is precisely the mathemat ...
... one of the seven basic assumptions out of which calculus flows. The statements that we assume true (in order to form a starting point for logical deductions) are called axioms. My dictionary 1 defines an axiom to be a “proposition regarded as a self-evident truth”, and this is precisely the mathemat ...
Polar Coordinates and Complex Numbers Infinite Series Vectors
... adding to numbers or functions that nobody has heard of. The situation was the same for integrals-they give famous answers like In x or unknown answers like 1xXdx. The sum of 1 + 118 + 1/27 + is also unknown-although a lot of mathematicians have tried. The chapter is not long, but it is full. The la ...
... adding to numbers or functions that nobody has heard of. The situation was the same for integrals-they give famous answers like In x or unknown answers like 1xXdx. The sum of 1 + 118 + 1/27 + is also unknown-although a lot of mathematicians have tried. The chapter is not long, but it is full. The la ...
GACE Review - Kennesaw State University College of Science and
... – Derivatives – A derivative is the slope of the line tangent to the curve at a point. It is the instantaneous rate y is changing per unit change in x. (So you’re already intimate with derivatives of linear functions …) Recall that the second derivative is acceleration. – If the function is increasi ...
... – Derivatives – A derivative is the slope of the line tangent to the curve at a point. It is the instantaneous rate y is changing per unit change in x. (So you’re already intimate with derivatives of linear functions …) Recall that the second derivative is acceleration. – If the function is increasi ...
Mathematics 1 - University of London International Programmes
... problem and know that it is solved. Unlike many of the other subjects you will study, there is always a right answer in mathematics problems. Of course, part of the excitement of the social sciences arises from the fact that there may be no single ‘right answer’ to a problem: it is stimulating to pa ...
... problem and know that it is solved. Unlike many of the other subjects you will study, there is always a right answer in mathematics problems. Of course, part of the excitement of the social sciences arises from the fact that there may be no single ‘right answer’ to a problem: it is stimulating to pa ...
Infinitesimals Abstract
... That line includes the real numbers separated by the nonconstant hyper-reals. Each real number is the center of an interval of hyper-reals, that includes no other real number. In particular, zero is separated from any positive real by the positive infinitesimals, and from any negative real by the ne ...
... That line includes the real numbers separated by the nonconstant hyper-reals. Each real number is the center of an interval of hyper-reals, that includes no other real number. In particular, zero is separated from any positive real by the positive infinitesimals, and from any negative real by the ne ...
Integral calculus, and introduction to analysis
... Example 1.2.5. (A silly example) In a hotel, keys for all the guest rooms are kept on hooks behind the reception desk. If a room is occupied, the key is missing from its hook because the guests have it. If the receptionist wants to know how many rooms are occupied, s/he doesn’t have to visit all th ...
... Example 1.2.5. (A silly example) In a hotel, keys for all the guest rooms are kept on hooks behind the reception desk. If a room is occupied, the key is missing from its hook because the guests have it. If the receptionist wants to know how many rooms are occupied, s/he doesn’t have to visit all th ...
Presentation Version - Parkway C-2
... Objectives: 1. Be able to apply the first derivative test to find relative extrema of a function Critical Vocabulary: Increasing, Decreasing, Constant Warm Up: Determine (using calculus) where each function is increasing, decreasing, and constant. 1. f(x) = 2x3 - 3x2 - 36x + 14 ...
... Objectives: 1. Be able to apply the first derivative test to find relative extrema of a function Critical Vocabulary: Increasing, Decreasing, Constant Warm Up: Determine (using calculus) where each function is increasing, decreasing, and constant. 1. f(x) = 2x3 - 3x2 - 36x + 14 ...
f ``(x)
... sale of x units of a certain prescription drug is given by P(x) = ln(-x3 + 3x2 + 72x + 1) for x in [0, 10]. ...
... sale of x units of a certain prescription drug is given by P(x) = ln(-x3 + 3x2 + 72x + 1) for x in [0, 10]. ...
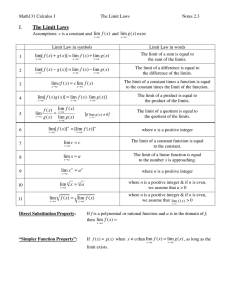
Chapter 2: Limits and Continuity
... We start with a number c and a function f defined at all numbers x near c but not necessarily at c itself. In any case, whether or not f is defined at c and, if so, how is totally irrelevant. Now let L be some real number. We say that the limit of f (x) as x tends to c is L and write lim f x L ...
... We start with a number c and a function f defined at all numbers x near c but not necessarily at c itself. In any case, whether or not f is defined at c and, if so, how is totally irrelevant. Now let L be some real number. We say that the limit of f (x) as x tends to c is L and write lim f x L ...
Chapter 2: Limits and Continuity
... We start with a number c and a function f defined at all numbers x near c but not necessarily at c itself. In any case, whether or not f is defined at c and, if so, how is totally irrelevant. Now let L be some real number. We say that the limit of f (x) as x tends to c is L and write lim f x L ...
... We start with a number c and a function f defined at all numbers x near c but not necessarily at c itself. In any case, whether or not f is defined at c and, if so, how is totally irrelevant. Now let L be some real number. We say that the limit of f (x) as x tends to c is L and write lim f x L ...
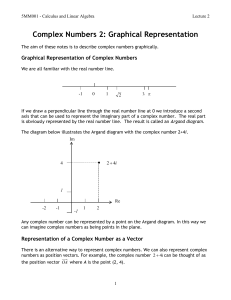
Document
... Graph of a Function: The set of all points (x, f (x)) where x is the domain of f (x). Generally, this forms a curve in the xyplane. ...
... Graph of a Function: The set of all points (x, f (x)) where x is the domain of f (x). Generally, this forms a curve in the xyplane. ...
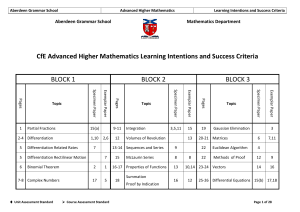
CfE AH LI and SC Booklet - Aberdeen Grammar School
... I can find the roots of a quartic when one complex root is given. I can factorise polynomials with real coefficients. I can find the square root of a complex number. I can solve equations involving complex numbers by equating real and imaginary parts. 6) Show that z 3 3i is a root of the equation ...
... I can find the roots of a quartic when one complex root is given. I can factorise polynomials with real coefficients. I can find the square root of a complex number. I can solve equations involving complex numbers by equating real and imaginary parts. 6) Show that z 3 3i is a root of the equation ...
Math 201-103-RE Practice Assignment 5 Applications of the
... (30) A Tire Company has 20 stores on the island of Montreal, each of which has an average income of $7000 per week. After study, the company notices that for each new store opened, the average weekly income drops $70. How many new stores should be opened to maximize income? (31) The average cost in ...
... (30) A Tire Company has 20 stores on the island of Montreal, each of which has an average income of $7000 per week. After study, the company notices that for each new store opened, the average weekly income drops $70. How many new stores should be opened to maximize income? (31) The average cost in ...