HW Day #13 Answers
... 16. A jar contains black and white marbles. Two marbles are chosen without replacement. The probability of selecting a black marble and then a white marble is 0.34, and the probability of selecting a black marble on the first draw is 0.47. What is the probability of selecting a white marble on the s ...
... 16. A jar contains black and white marbles. Two marbles are chosen without replacement. The probability of selecting a black marble and then a white marble is 0.34, and the probability of selecting a black marble on the first draw is 0.47. What is the probability of selecting a white marble on the s ...
Several Random Variables
... set functions (E) = P(T E and R s) and (E) = P(T E)P(R s). It is not hard to see that they are both measures. Since they agree for sets E of the form {T t} they must agree for all Borel sets. Therefore P(T E and R s) = P(T E)P(R s) for all Borel sets E. A similar argument shows P ...
... set functions (E) = P(T E and R s) and (E) = P(T E)P(R s). It is not hard to see that they are both measures. Since they agree for sets E of the form {T t} they must agree for all Borel sets. Therefore P(T E and R s) = P(T E)P(R s) for all Borel sets E. A similar argument shows P ...
311 review sheet. The exam covers sections 3.4, 3.5, 3.6, 3.7, 3.8
... The exam covers sections 3.4, 3.5, 3.6, 3.7, 3.8, 4.1, 4.2, 4.3, 4.4, and 4.6 from the text. Sections 4.1 and 4.2 cover general theory about continuous random variables. Otherwise the material covers some named distributions: the geometric, the negative binomial, the Poisson, the hypergeometric, the ...
... The exam covers sections 3.4, 3.5, 3.6, 3.7, 3.8, 4.1, 4.2, 4.3, 4.4, and 4.6 from the text. Sections 4.1 and 4.2 cover general theory about continuous random variables. Otherwise the material covers some named distributions: the geometric, the negative binomial, the Poisson, the hypergeometric, the ...
f7ch6
... the probability that he misses is q, where q = 1 – p. Write an expression for the probability that, in 10 shots, he hits the target 6 times. If the probability that an experiment results in a successful outcome is p and the probability that the outcome is a failure is q, where q = 1 – p, and if X is ...
... the probability that he misses is q, where q = 1 – p. Write an expression for the probability that, in 10 shots, he hits the target 6 times. If the probability that an experiment results in a successful outcome is p and the probability that the outcome is a failure is q, where q = 1 – p, and if X is ...
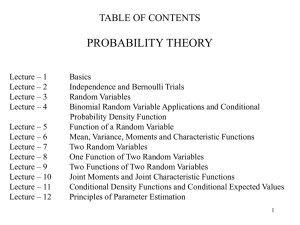
Lecture3
... 1. Intuitively, the entropy of X is the amount of information it encodes, measured in bits. There are theorems that justify this interpretation, saying that the average number of bits needed to encode X’s value is exactly H(X). 2. For any random variable X taking on n possible values there holds H(X ...
... 1. Intuitively, the entropy of X is the amount of information it encodes, measured in bits. There are theorems that justify this interpretation, saying that the average number of bits needed to encode X’s value is exactly H(X). 2. For any random variable X taking on n possible values there holds H(X ...
6.1 Discrete and Continuous Random Variables
... their probabilities. • Probability distributions could be in table or histogram form. Example: Let’s define the random variable X as the number of games played in a randomly selected World Series. As a histogram: Its probability distribution: ...
... their probabilities. • Probability distributions could be in table or histogram form. Example: Let’s define the random variable X as the number of games played in a randomly selected World Series. As a histogram: Its probability distribution: ...
Statistics
... has already occurred or we have some extra information about the event...this, of course, may affect the probability of the event Example 17: You roll a die, I see the result and tell you that it is an even number. What is the probability that number 6 shows up? Example 18: You are to guess on the p ...
... has already occurred or we have some extra information about the event...this, of course, may affect the probability of the event Example 17: You roll a die, I see the result and tell you that it is an even number. What is the probability that number 6 shows up? Example 18: You are to guess on the p ...
Bayes` Rule
... The probability that Mary picks a red flower if she chooses a plot at random is 16/35 Note: the two different results for part (a) and part (b) are slightly surprising. In the first case, there is one group of flowers and each flower is equally likely to be chosen. In the second case, even though ea ...
... The probability that Mary picks a red flower if she chooses a plot at random is 16/35 Note: the two different results for part (a) and part (b) are slightly surprising. In the first case, there is one group of flowers and each flower is equally likely to be chosen. In the second case, even though ea ...
2.2 Let E and F be two events for which one knows that the
... a. P(A ∪ B) if it is given that P(A) = 1/3 and P(B | Ac ) = 1/4. b. P(B) if it is given that P(A ∪ B) = 2/3 and P(Ac | B c ) = 1/2. 3.8 ! Spaceman Spiff’s spacecraft has a warning light that is supposed to switch on when the freem blasters are overheated. Let W be the event “the warning light is swit ...
... a. P(A ∪ B) if it is given that P(A) = 1/3 and P(B | Ac ) = 1/4. b. P(B) if it is given that P(A ∪ B) = 2/3 and P(Ac | B c ) = 1/2. 3.8 ! Spaceman Spiff’s spacecraft has a warning light that is supposed to switch on when the freem blasters are overheated. Let W be the event “the warning light is swit ...
chapter 5 the binomial probability distribution
... 1. You toss a coin 8 times. Call heads success. If the coin is fair, the probability of success P is 0.5. What is the probability of getting exactly 5 heads out of 8 tosses? of exactly 20 heads out of 100 tosses? 2. A bank examiner’s record shows that the probability of an error in a statement for a ...
... 1. You toss a coin 8 times. Call heads success. If the coin is fair, the probability of success P is 0.5. What is the probability of getting exactly 5 heads out of 8 tosses? of exactly 20 heads out of 100 tosses? 2. A bank examiner’s record shows that the probability of an error in a statement for a ...
prob_distr_disc
... 1. In each part, indicate, (1) whether the variable is discrete or continuous AND (2) whether it is binomial or not AND (3) if it is binomial, give values for n and p. a. Number of times a “head” comes up in 10 flips of a coin 1. Discrete or continuous 2. Binomial yes or no 3. If Binomial what is n ...
... 1. In each part, indicate, (1) whether the variable is discrete or continuous AND (2) whether it is binomial or not AND (3) if it is binomial, give values for n and p. a. Number of times a “head” comes up in 10 flips of a coin 1. Discrete or continuous 2. Binomial yes or no 3. If Binomial what is n ...
Statistics-1
... Example: event A: die 16, event B: die 24, P(A)=1/6, P(B)=1/6, two independent events, P(A and B)= P(A)P(B)=(1/6)(1/6)=1/36 Mutual exclusive: outcome of A will exclude outcome of B and vice versa Joint probability both A & B occur: P(A and B) = P(AB) = P(A)P(B) = P(BA) for independent events ...
... Example: event A: die 16, event B: die 24, P(A)=1/6, P(B)=1/6, two independent events, P(A and B)= P(A)P(B)=(1/6)(1/6)=1/36 Mutual exclusive: outcome of A will exclude outcome of B and vice versa Joint probability both A & B occur: P(A and B) = P(AB) = P(A)P(B) = P(BA) for independent events ...
What are the Eigenvalues of a Sum of Non
... • depends on joint densities and • (covariance of eigenvalues matters!) • Real β=1, complex β=2, (quaternion, ghost…) matters ...
... • depends on joint densities and • (covariance of eigenvalues matters!) • Real β=1, complex β=2, (quaternion, ghost…) matters ...
Lecture 2: Simple Bayesian Networks
... P (E|S&D) = αP (E)P (S|E)P (D|E) Immediately we have a problem, since we do not have a direct estimate for P (E), the prior probability of the eyes. E is an intermediate variable that we compute and we are not measuring it. However, we can still calculate a likelihood value of E. A likelihood value ...
... P (E|S&D) = αP (E)P (S|E)P (D|E) Immediately we have a problem, since we do not have a direct estimate for P (E), the prior probability of the eyes. E is an intermediate variable that we compute and we are not measuring it. However, we can still calculate a likelihood value of E. A likelihood value ...