§3.2 – Conditional Probability and Independence
... probability that the card is from the diamond suit is 1/4, but if you knew somehow that the card was red, then the probability would jump to 1/2. We say that the conditional probability of “diamond” given “red” is 1/2. The symbolism for this is Pr(A|B) which we read as “the conditional probability o ...
... probability that the card is from the diamond suit is 1/4, but if you knew somehow that the card was red, then the probability would jump to 1/2. We say that the conditional probability of “diamond” given “red” is 1/2. The symbolism for this is Pr(A|B) which we read as “the conditional probability o ...
BROWNIAN MOTION Definition 1. A standard Brownian (or a
... and let {Ft∗ }t ≥0 be the filtration of the process {W ∗ (t )}t ≥0 . Then (a) {W ∗ (t )}t ≥0 is a standard Brownian motion; and (b) For each t > 0, the σ−algebra Ft∗ is independent of Fτ . Details of the proof are omitted (see, for example, K ARATZAS & S HREVE, pp. 79ff). Let’s discuss briefly the m ...
... and let {Ft∗ }t ≥0 be the filtration of the process {W ∗ (t )}t ≥0 . Then (a) {W ∗ (t )}t ≥0 is a standard Brownian motion; and (b) For each t > 0, the σ−algebra Ft∗ is independent of Fτ . Details of the proof are omitted (see, for example, K ARATZAS & S HREVE, pp. 79ff). Let’s discuss briefly the m ...
The Poisson process Math 217 Probability and Statistics
... P10 (t) = −λP1 (t) + λe−λt . That’s not such an elementary equation as the first one, but it’s what’s called a linear differential equation, and it can be solved by elementary methods. Along with the initial value P1 (0) = 0, there’s a unique solution which is P1 (t) = λte−t . In general, if we let ...
... P10 (t) = −λP1 (t) + λe−λt . That’s not such an elementary equation as the first one, but it’s what’s called a linear differential equation, and it can be solved by elementary methods. Along with the initial value P1 (0) = 0, there’s a unique solution which is P1 (t) = λte−t . In general, if we let ...
3.3 The Dominated Convergence Theorem
... because of the Skorohod Representation Theorem.) Show that if Xn = |Zn − Z|, then X1 , X2 , . . . is a uniformly integrable sequence. Hint: Use Fatou’s Lemma (Exercise 3.11) to show that E |Z| < ∞, i.e., Z is integrable. Then use part (a). (c) By part (b), the desired result now follows from the fol ...
... because of the Skorohod Representation Theorem.) Show that if Xn = |Zn − Z|, then X1 , X2 , . . . is a uniformly integrable sequence. Hint: Use Fatou’s Lemma (Exercise 3.11) to show that E |Z| < ∞, i.e., Z is integrable. Then use part (a). (c) By part (b), the desired result now follows from the fol ...
Infinite Markov chains, continuous time Markov chains
... but different in other respects. We denote again by pi,j the probability of transition from state i to state j. We introduce the notion of i communicates with j, written as i → j, in the same manner as before. Thus again we may decompose the state space into states i such that for some j, i → j but j ...
... but different in other respects. We denote again by pi,j the probability of transition from state i to state j. We introduce the notion of i communicates with j, written as i → j, in the same manner as before. Thus again we may decompose the state space into states i such that for some j, i → j but j ...
Generating Graphoids from Generalised Conditional Probability
... be a semi-graphoid. As we shall see in section 5, probabilistic conditional independence is a semi-graphoid, and in certain situations a graphoid. The definitions given here for semi-graphoid and graphoid differ from that given in [Pearl, 88], in that we require Trivial Independence to hold. However ...
... be a semi-graphoid. As we shall see in section 5, probabilistic conditional independence is a semi-graphoid, and in certain situations a graphoid. The definitions given here for semi-graphoid and graphoid differ from that given in [Pearl, 88], in that we require Trivial Independence to hold. However ...
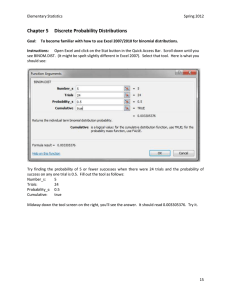
Chapter 5 Discrete Probability Distributions
... event. We typically use capital letters like A or B. Therefore if A is the event that we roll a seven all of the following are equivalent: ...
... event. We typically use capital letters like A or B. Therefore if A is the event that we roll a seven all of the following are equivalent: ...
DevStat8e_04_01
... a randomly chosen point on the surface. Let M = the maximum depth (in meters), so that any number in the interval [0, M] is a possible value of X. If we “discretize” X by measuring depth to the nearest meter, then possible values are nonnegative integers less than or equal to M. The resulting discre ...
... a randomly chosen point on the surface. Let M = the maximum depth (in meters), so that any number in the interval [0, M] is a possible value of X. If we “discretize” X by measuring depth to the nearest meter, then possible values are nonnegative integers less than or equal to M. The resulting discre ...
Notes Binomial
... • Given a discrete random variable X, the probability distribution function assigns a probability to each value of X. The probabilities must satisfy the rules for probabilities given in Chapter 6. • The command binompdf(n,p,X) calculates the binomial probability of the value X. It is ...
... • Given a discrete random variable X, the probability distribution function assigns a probability to each value of X. The probabilities must satisfy the rules for probabilities given in Chapter 6. • The command binompdf(n,p,X) calculates the binomial probability of the value X. It is ...
(pdf)
... Theorem 2.2 (Weak Law of Large Numbers) If X1 , X2 , . . . , Xn are independent and identically distributed with a finite first moment and E(Xi ) = m < ∞, then X1 +X2n+···+Xn converges to m in probability as n → ∞. Theorem 2.3 (Strong Law of Large Numbers) If X1 , X2 , . . . , Xn are independent and ...
... Theorem 2.2 (Weak Law of Large Numbers) If X1 , X2 , . . . , Xn are independent and identically distributed with a finite first moment and E(Xi ) = m < ∞, then X1 +X2n+···+Xn converges to m in probability as n → ∞. Theorem 2.3 (Strong Law of Large Numbers) If X1 , X2 , . . . , Xn are independent and ...
Targil 10
... are always n – 1 and not n. I think the aesthetic reason for that definition was that m n people prefer to get the formula m, n and not m + n + 1 below. m n There are also some ideological reasons for this (they say it is Mellin transform, which is version of Fourier for mul ...
... are always n – 1 and not n. I think the aesthetic reason for that definition was that m n people prefer to get the formula m, n and not m + n + 1 below. m n There are also some ideological reasons for this (they say it is Mellin transform, which is version of Fourier for mul ...
Crash course in probability theory and statistics – part 1
... and satisfies p(X=x i) ³ 0 for all i, åi p(X=xi) = 1, and for any subset { xjWe often simplify the notation and use both } Í { xi }: p(XÎ{xj}) = åjp(xj) . p(X) The definitions are pure abstract math. Any real world usefulness is pure luck. and p(x i) for p(X=xi), depending on context. In ...
... and satisfies p(X=x i) ³ 0 for all i, åi p(X=xi) = 1, and for any subset { xjWe often simplify the notation and use both } Í { xi }: p(XÎ{xj}) = åjp(xj) . p(X) The definitions are pure abstract math. Any real world usefulness is pure luck. and p(x i) for p(X=xi), depending on context. In ...