Final Exam Review Basic Topics covered Unit 1 Basic terms of
... Unit 4 we have already discussed most of this in the first unit so not much of it will be ne or unknown ...
... Unit 4 we have already discussed most of this in the first unit so not much of it will be ne or unknown ...
High School Geometry Mathematics Curriculum
... Use coordinates to prove simple geometric • Use coordinates to prove simple geometric theorems algebraically. For example, prove theorems algebraically or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the ...
... Use coordinates to prove simple geometric • Use coordinates to prove simple geometric theorems algebraically. For example, prove theorems algebraically or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the ...
Right Triangles and the Unit Circle - Golden GSE Pre
... 5. Which of your two triangles can be reflected to create the angle in the third quadrant with a 30o reference angle? What is this angle measure? Complete this reflection. Mark the lengths of the three legs of the third quadrant triangle on your graph. What are the coordinates of the new point on ci ...
... 5. Which of your two triangles can be reflected to create the angle in the third quadrant with a 30o reference angle? What is this angle measure? Complete this reflection. Mark the lengths of the three legs of the third quadrant triangle on your graph. What are the coordinates of the new point on ci ...
Name - mrshayden
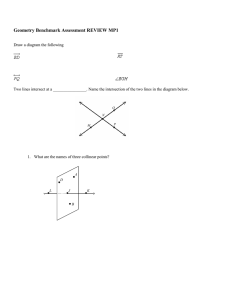
... name for GH 33.________________Give another name for plane CDE 34.________________Where do plane DCE and GI intersect? ...
... name for GH 33.________________Give another name for plane CDE 34.________________Where do plane DCE and GI intersect? ...
Name: Date: Core-Geo: 2.2ConditionalStatements Warm
... To write the ________________of a conditional statement, switch the ____________ and the _______________________ of the statement. This does not include switching the key words, _____ and ________. Ex. 2 Converses Write the converse of each conditional statement below. Is the converse true or false? ...
... To write the ________________of a conditional statement, switch the ____________ and the _______________________ of the statement. This does not include switching the key words, _____ and ________. Ex. 2 Converses Write the converse of each conditional statement below. Is the converse true or false? ...
Ch 1 Review - Stevenson High School
... Use the diagram to identify the following: a. Name a pair of adjacent angles. b. Name a pair of vertical angles. c. Name a linear pair. d. Name a pair of congruent angles. ...
... Use the diagram to identify the following: a. Name a pair of adjacent angles. b. Name a pair of vertical angles. c. Name a linear pair. d. Name a pair of congruent angles. ...
Vocabulary Flash Cards (part 2)
... A formal proof in which statements are listed in one column and the reasons for each statement are listed in a second column. ...
... A formal proof in which statements are listed in one column and the reasons for each statement are listed in a second column. ...
Slide 1
... A. Yes, it is a regular quadrilateral because all sides are the same length. B. Yes, it is a regular quadrilateral because the diagonals are perpendicular. C. No, it is not a regular quadrilateral because RSTU is not a parallelogram. D. No, it is not a regular quadrilateral because the diagonals are ...
... A. Yes, it is a regular quadrilateral because all sides are the same length. B. Yes, it is a regular quadrilateral because the diagonals are perpendicular. C. No, it is not a regular quadrilateral because RSTU is not a parallelogram. D. No, it is not a regular quadrilateral because the diagonals are ...
Geometry Observation for Continued
... h. Recognize and use the symbols of formal logic, which include , , , , ∧, and ∨ G.2 Overall Score a. Use algebraic and coordinate methods as well as deductive proofs to verify whether two lines are parallel b. Solve problems by using the relationships between pairs of angles formed by the inter ...
... h. Recognize and use the symbols of formal logic, which include , , , , ∧, and ∨ G.2 Overall Score a. Use algebraic and coordinate methods as well as deductive proofs to verify whether two lines are parallel b. Solve problems by using the relationships between pairs of angles formed by the inter ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.