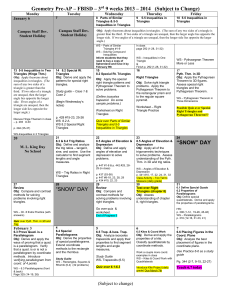
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... A circle may be constructed with any centre and radius. ...
... A circle may be constructed with any centre and radius. ...
Plane Geometry - UVa-Wise
... really seems quite out of place. Almost from the time of Euclid through much of the nineteenth century, there was significant effort to expunge the fifth postulate from the list by proving it as a theorem resulting from the other four. These efforts ultimately failed (opening the door for non-Euclid ...
... really seems quite out of place. Almost from the time of Euclid through much of the nineteenth century, there was significant effort to expunge the fifth postulate from the list by proving it as a theorem resulting from the other four. These efforts ultimately failed (opening the door for non-Euclid ...
The Project Gutenberg eBook #29807: Solid Geometry
... is assumed that the whole figure need not lie in any one plane. Thus, in plane geometry we have the theorem: “Through a fixed point on a line one and only one perpendicular can be drawn to the line.” ...
... is assumed that the whole figure need not lie in any one plane. Thus, in plane geometry we have the theorem: “Through a fixed point on a line one and only one perpendicular can be drawn to the line.” ...
Parallel and Perpendicular Lines
... Lines must be marked parallel with the arrows in order to say they are parallel. Just because two lines LOOK parallel, does not mean that they are. Recall the definition of perpendicular from Chapter 1. Two lines are perpendicular when they intersect to form a 90◦ angle. Below l ⊥ AB. ...
... Lines must be marked parallel with the arrows in order to say they are parallel. Just because two lines LOOK parallel, does not mean that they are. Recall the definition of perpendicular from Chapter 1. Two lines are perpendicular when they intersect to form a 90◦ angle. Below l ⊥ AB. ...
Congruence - Kids at the Core
... If the pentagon below is rotated clockwise around its center, the minimum number of degrees it must be rotated to carry the pentagon onto itself is... ...
... If the pentagon below is rotated clockwise around its center, the minimum number of degrees it must be rotated to carry the pentagon onto itself is... ...
Congruency, Similarity, Right Triangles
... A connected straight path. It has no thickness and it continues forever in both directions. ...
... A connected straight path. It has no thickness and it continues forever in both directions. ...
CHAPTER 3 Parallel and Perpendicular Lines
... 25. Skew Lines Algebra Connection In questions 26-35 we will begin to explore the concepts of parallel and perpendicular lines in the coordinate plane. Write the equations of two lines parallel to y = 3. Write the equations of two lines perpendicular to y = 5. What is the relationship between the tw ...
... 25. Skew Lines Algebra Connection In questions 26-35 we will begin to explore the concepts of parallel and perpendicular lines in the coordinate plane. Write the equations of two lines parallel to y = 3. Write the equations of two lines perpendicular to y = 5. What is the relationship between the tw ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.