Complex Numbers
... In section 3.5 of the textbook complex numbers are introduced, along with the operations of addition, subtraction, multiplication, and division of complex numbers. Here we will look at the geometric interpretation of complex numbers, the absolute value and argument of a complex number, and time perm ...
... In section 3.5 of the textbook complex numbers are introduced, along with the operations of addition, subtraction, multiplication, and division of complex numbers. Here we will look at the geometric interpretation of complex numbers, the absolute value and argument of a complex number, and time perm ...
Progression in multiplication - Geoffrey Field Infant School
... Count in 2s, 10s, 5s, 3s and 4s, recording on a number line Begin to recognise these as tables facts ...
... Count in 2s, 10s, 5s, 3s and 4s, recording on a number line Begin to recognise these as tables facts ...
Lecture 15
... Swap the tails at the fault line to map to a tiling of 2 n-1 ‘s to a tiling of an n-2 and an n. ...
... Swap the tails at the fault line to map to a tiling of 2 n-1 ‘s to a tiling of an n-2 and an n. ...
Brief review of complex numbers 1 Representations
... Imaginary and complex numbers We start by introducing a symbol i that represents the squareroot of −1, i.e., i 2 = −1. For some strange reason, electrical engineers use the symbol j instead of i. (Maybe because i could be confused with current?) It’s a dumb tradition, but I’ll respect it here. We re ...
... Imaginary and complex numbers We start by introducing a symbol i that represents the squareroot of −1, i.e., i 2 = −1. For some strange reason, electrical engineers use the symbol j instead of i. (Maybe because i could be confused with current?) It’s a dumb tradition, but I’ll respect it here. We re ...
Session 13 – Exponents and Simplifying Expressions Which would
... different answers. Some may multiply first then add to obtain 29 and another person might add first then multiple to obtain 44. This situation is unacceptable. So, people have agreed on certain standard rules for determining the value of expressions that involve different operations. The most common ...
... different answers. Some may multiply first then add to obtain 29 and another person might add first then multiple to obtain 44. This situation is unacceptable. So, people have agreed on certain standard rules for determining the value of expressions that involve different operations. The most common ...
Numbers and Vectors - University of Leeds
... This proves that the Inequality (6) is correct. Putting it all together we have proved Lemma 1 using mathematical induction. ...
... This proves that the Inequality (6) is correct. Putting it all together we have proved Lemma 1 using mathematical induction. ...
Math Vocabulary 3-1 - Clinton Public Schools
... addends- Numbers added together to give a sum. Example: 7 + 5 = 12 addend + addend = sum sum-The answer when adding two or more addends. Example: 7 + 5 = 12 addend + addend = sum difference- The answer when subtracting two numbers. Example: 7 – 2 = 5 factors- Numbers that are multiplied to give a pr ...
... addends- Numbers added together to give a sum. Example: 7 + 5 = 12 addend + addend = sum sum-The answer when adding two or more addends. Example: 7 + 5 = 12 addend + addend = sum difference- The answer when subtracting two numbers. Example: 7 – 2 = 5 factors- Numbers that are multiplied to give a pr ...
Section 1.5
... parentheses, and then perform the multiplication, or you can use the distributive property, and then simplify. However, if the quantity inside the parenthesis contains “unlike quantities”, you can’t do the addition or subtraction first, so you must use the distributive property in order to simplif ...
... parentheses, and then perform the multiplication, or you can use the distributive property, and then simplify. However, if the quantity inside the parenthesis contains “unlike quantities”, you can’t do the addition or subtraction first, so you must use the distributive property in order to simplif ...
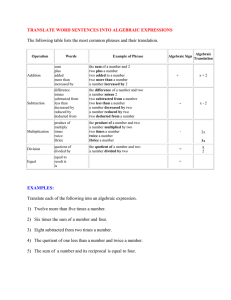
Number and Quality - Singapore American School
... Extend the properties of exponents to rational exponents. HSN.RN.1 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents to those values, allo ...
... Extend the properties of exponents to rational exponents. HSN.RN.1 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents to those values, allo ...
Guidelines for Preparing a Paper for the European Conference on
... doubling technique [9, pp. 56–61], would require the same number of steps as the RCB requires. If either the row or column of the originator and target processors are the same then the message will travel only in a horizontal or vertical direction, respectively (see [12]). ...
... doubling technique [9, pp. 56–61], would require the same number of steps as the RCB requires. If either the row or column of the originator and target processors are the same then the message will travel only in a horizontal or vertical direction, respectively (see [12]). ...
Guidelines for Preparing a Paper for European Conference on
... of s = N=P elements each. We assume without loss of generality that N is an integer multiple of P . We define each subset as Wp = s (p 1)s + j j =1 (see [11], [4] and [2] for details). Each processor p is responsible for performing the computations over the variables contained in Wp . In the case of ...
... of s = N=P elements each. We assume without loss of generality that N is an integer multiple of P . We define each subset as Wp = s (p 1)s + j j =1 (see [11], [4] and [2] for details). Each processor p is responsible for performing the computations over the variables contained in Wp . In the case of ...