Lecture 12 — March 21, 2007 1 Overview 2 Models of Computation
... that either S[high(x)] was already nonempty, so nothing in the summary changes and we just recurse in S[high(x)], or S[high(x)] was empty, and we need to insert high(x) recursively in the summary, but insertion into S[high(x)] is trivial (so we don’t need a second recursive call, which would blow up ...
... that either S[high(x)] was already nonempty, so nothing in the summary changes and we just recurse in S[high(x)], or S[high(x)] was empty, and we need to insert high(x) recursively in the summary, but insertion into S[high(x)] is trivial (so we don’t need a second recursive call, which would blow up ...
Document
... The children of any node in a tree can be accessed by following only one branch path, the one that leads to the desired node. The nodes at level 1, which are children of the root, can be accessed by following only one branch; the nodes of level 2 of a tree can be accessed by following only two branc ...
... The children of any node in a tree can be accessed by following only one branch path, the one that leads to the desired node. The nodes at level 1, which are children of the root, can be accessed by following only one branch; the nodes of level 2 of a tree can be accessed by following only two branc ...
Overview and History
... void remove(const Item & desiredItem) // Assumes: desired is stored in the tree, Item supports relational ops // Results: first occurrence of desiredItem is removed from tree ...
... void remove(const Item & desiredItem) // Assumes: desired is stored in the tree, Item supports relational ops // Results: first occurrence of desiredItem is removed from tree ...
OrderedMap with a BST Data Structure - University of Arizona
... Binary Search Trees A Binary Search Tree (BST) data structure is a binary tree with an ordering property BSTs are used to maintain order and faster retrieval, insertion, and removal of individual elements A Binary Search Tree (BST) is ...
... Binary Search Trees A Binary Search Tree (BST) data structure is a binary tree with an ordering property BSTs are used to maintain order and faster retrieval, insertion, and removal of individual elements A Binary Search Tree (BST) is ...
thm01 - persistent ds_1
... Application: Planar point location Suppose that the Euclidian plane is subdivided into polygons by n line segments that intersect only at their endpoints. Given such a polygonal subdivision and an on-line sequence of query points in the plane, the planar point location problem, is to determine for ...
... Application: Planar point location Suppose that the Euclidian plane is subdivided into polygons by n line segments that intersect only at their endpoints. Given such a polygonal subdivision and an on-line sequence of query points in the plane, the planar point location problem, is to determine for ...
Data Structures Lecture 1
... Growable Array-based Array List In an add(o) operation (without an index), we always add at the end When the array is full, we replace the array with a larger one How large should the new array be? Incremental strategy: increase the size by a ...
... Growable Array-based Array List In an add(o) operation (without an index), we always add at the end When the array is full, we replace the array with a larger one How large should the new array be? Incremental strategy: increase the size by a ...
Advance Data Structures and Algorithms
... Binary trees are non-linear hierarchical data structures where every component may have one super-component directly above and no more than two subcomponents directly below They are finite sets of one or more linked nodes, linked by lines called branches Except when the tree is empty, there is a spe ...
... Binary trees are non-linear hierarchical data structures where every component may have one super-component directly above and no more than two subcomponents directly below They are finite sets of one or more linked nodes, linked by lines called branches Except when the tree is empty, there is a spe ...
exam
... vertex in the graph, starting from any vertex v ∈ V0 . Explain briefly how to use or modify the shortest-path algorithm obtain this distance instead. For full credit your solution should be asymptotically as efficient as Dijkstra’s algorithm. 5. Trees [14 pts] ...
... vertex in the graph, starting from any vertex v ∈ V0 . Explain briefly how to use or modify the shortest-path algorithm obtain this distance instead. For full credit your solution should be asymptotically as efficient as Dijkstra’s algorithm. 5. Trees [14 pts] ...
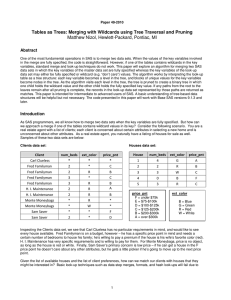
Tables As Trees: Merging with Wildcards Using Tree Traversal and Pruning
... Because a tree structure is typically dynamic and can grow and shrink over time, programmers traditionally use dynamic memory allocation to store trees. The structure of a single node is determined by the programmer, and then nodes are created and destroyed on an as-needed basis during program run-t ...
... Because a tree structure is typically dynamic and can grow and shrink over time, programmers traditionally use dynamic memory allocation to store trees. The structure of a single node is determined by the programmer, and then nodes are created and destroyed on an as-needed basis during program run-t ...
CS 61B Data Structures and Programming Methodology
... immediately (constant time) if x is in the set. • What’s a situation where you can determine set membership in constant time? – The set contains integers with bounded values, i.e. for every x in the set, L < x < R, and L and R are known. ...
... immediately (constant time) if x is in the set. • What’s a situation where you can determine set membership in constant time? – The set contains integers with bounded values, i.e. for every x in the set, L < x < R, and L and R are known. ...
Lecture - Binary Tree - Home
... Binary trees naturally arise in many different applications 1. Expression Tree - A central data structure in compiler design - Interior nodes contain operators and the leaf nodes have operands - An expression is evaluated by applying the operator at root to the values obtained by recursively evalu ...
... Binary trees naturally arise in many different applications 1. Expression Tree - A central data structure in compiler design - Interior nodes contain operators and the leaf nodes have operands - An expression is evaluated by applying the operator at root to the values obtained by recursively evalu ...
Slide 1
... Integer-doubly linked list : A temporary variable (ex. el) is set to the value in the node. 2. tail is set to its predecessor. 3. The last node is deleted. 4. The next member of the tail node is set to null. 5. Return the copy of the object stored in the removed node. Note : before deleting, check ...
... Integer-doubly linked list : A temporary variable (ex. el) is set to the value in the node. 2. tail is set to its predecessor. 3. The last node is deleted. 4. The next member of the tail node is set to null. 5. Return the copy of the object stored in the removed node. Note : before deleting, check ...
Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. Bentley in 1974. A similar partitioning is also known as a Q-tree. All forms of quadtrees share some common features: They decompose space into adaptable cells Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits The tree directory follows the spatial decomposition of the quadtree.