Data Structures for Dynamic Sets Operations on Dynamic Sets
... The BST property allows us to print out all keys in sorted order using a simple recursive algorithm called an inorder tree walk. Strategy: visit left(x), visit x, visit right(x) Inorder-Tree-Walk(x) /** start at root **/ 1. if x ≠ NIL then ...
... The BST property allows us to print out all keys in sorted order using a simple recursive algorithm called an inorder tree walk. Strategy: visit left(x), visit x, visit right(x) Inorder-Tree-Walk(x) /** start at root **/ 1. if x ≠ NIL then ...
PowerPoint
... taken off from the same end; last-in, firstout, LIFO • We can talk about the abstract data structure “stack” without knowing anything about the “values” that it stores: –Push means “save a value” –Pop means “get the value that was saved most ...
... taken off from the same end; last-in, firstout, LIFO • We can talk about the abstract data structure “stack” without knowing anything about the “values” that it stores: –Push means “save a value” –Pop means “get the value that was saved most ...
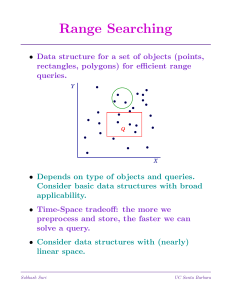
Range Searching
... • S1, S2, . . . , Sk are canonical subsets, Si ⊆ P , if the answer to any range query can be written as the disjoint union of some Si’s. • The canonical subsets may overlap. • Key is to determine correct Si’s, and given a query, efficiently determine the appropriate ones to use. • In 1D, a canonical ...
... • S1, S2, . . . , Sk are canonical subsets, Si ⊆ P , if the answer to any range query can be written as the disjoint union of some Si’s. • The canonical subsets may overlap. • Key is to determine correct Si’s, and given a query, efficiently determine the appropriate ones to use. • In 1D, a canonical ...
Computational Geometry: Proximity and Location
... Although many chains traverse the same edge, it suffices to store each edge only once in the structure, namely with the chain associated with the highest node in the binary tree. This is because once a discrimination of the query point is made with respect to such an edge, its relation is implicitly ...
... Although many chains traverse the same edge, it suffices to store each edge only once in the structure, namely with the chain associated with the highest node in the binary tree. This is because once a discrimination of the query point is made with respect to such an edge, its relation is implicitly ...
Abstract Data Types
... void queue.EnQueueFront(T value); O(1) link new node to Head void queue.EnQueueBack(T value); O(1) link new node to Tail T value = queue.DeQueueFront(); O(1) unlink Head else throw exception ...
... void queue.EnQueueFront(T value); O(1) link new node to Head void queue.EnQueueBack(T value); O(1) link new node to Tail T value = queue.DeQueueFront(); O(1) unlink Head else throw exception ...
Similar Triangles
... • Triangles are similar if they have the same shape, but not necessarily the same size • These triangles are all similar: ...
... • Triangles are similar if they have the same shape, but not necessarily the same size • These triangles are all similar: ...
Amortized Algorithm Analysis
... space after we need to make space allocate new O(k) array and copy elements – The time complexity of this worst-case depends on n, the size of the original array. How big should we make the new array? – There were n-1 simple operations in order to fill the array to this point, so let’s double it ...
... space after we need to make space allocate new O(k) array and copy elements – The time complexity of this worst-case depends on n, the size of the original array. How big should we make the new array? – There were n-1 simple operations in order to fill the array to this point, so let’s double it ...
Dr-Margush-06-07_LinkedLists
... • List keeps reference to last Node – Facilitates add to end since we always know where the last node is ...
... • List keeps reference to last Node – Facilitates add to end since we always know where the last node is ...
Parallel Synchronization-Free Approximate Data Structure
... In general, we expect the acceptability of the approximate data structures to depend on end-to-end effects such as 1) how frequently the application’s data structure construction workload elicits interactions that drop elements and 2) the effect that any dropped elements have on the accuracy of the ...
... In general, we expect the acceptability of the approximate data structures to depend on end-to-end effects such as 1) how frequently the application’s data structure construction workload elicits interactions that drop elements and 2) the effect that any dropped elements have on the accuracy of the ...
VBI-Tree: A Peer-to-Peer Framework for
... routing node maintains an “upside table”, with information about regions covered by each of its ancestors. Additionally, each node needs to keep information about heights of sub-trees rooted at its children. (This is used for the network restructuring process (see 6.1)). VBI-Tree construction employ ...
... routing node maintains an “upside table”, with information about regions covered by each of its ancestors. Additionally, each node needs to keep information about heights of sub-trees rooted at its children. (This is used for the network restructuring process (see 6.1)). VBI-Tree construction employ ...
Lecture 5 (linked lists, vectors)
... Since c is a constant, T(n) is O(n + k2), i.e., O(n2) The amortized time of a push operation is O(n) © 2004 Goodrich, Tamassia ...
... Since c is a constant, T(n) is O(n + k2), i.e., O(n2) The amortized time of a push operation is O(n) © 2004 Goodrich, Tamassia ...
Chapter 12 Greedy Algorithms for Minimum Spanning Trees
... makeQ: create an empty queue findMin: find the minimum key in S extractMin: Remove v ∈ S with smallest key and return it add(v, k(v)): Add new element v with key k(v) to S delete(v): Remove element v from S decreaseKey (v, k 0 (v)): decrease key of v from k(v) (current key) to k 0 (v) (new key). ...
... makeQ: create an empty queue findMin: find the minimum key in S extractMin: Remove v ∈ S with smallest key and return it add(v, k(v)): Add new element v with key k(v) to S delete(v): Remove element v from S decreaseKey (v, k 0 (v)): decrease key of v from k(v) (current key) to k 0 (v) (new key). ...
Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. Bentley in 1974. A similar partitioning is also known as a Q-tree. All forms of quadtrees share some common features: They decompose space into adaptable cells Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits The tree directory follows the spatial decomposition of the quadtree.