Wavelet Trees Meet Suffix Trees
... the bitmasks Bv , we do not remove the most significant bit of each character, and instead of partitioning the values based on this bit, we make a decision based on whether the leaf corresponding to the character lies in the left or in the right subtree of v. Our construction algorithm generalizes t ...
... the bitmasks Bv , we do not remove the most significant bit of each character, and instead of partitioning the values based on this bit, we make a decision based on whether the leaf corresponding to the character lies in the left or in the right subtree of v. Our construction algorithm generalizes t ...
Dynamic 3-sided planar range queries with expected - delab-auth
... hB-trees and various R-trees have been proposed. A recent survey can be found in [16]. Often these data structures are used in applications, because they are relatively simple, require linear space and perform well in practice most of the time. However, they all have highly sub-optimal worst case pe ...
... hB-trees and various R-trees have been proposed. A recent survey can be found in [16]. Often these data structures are used in applications, because they are relatively simple, require linear space and perform well in practice most of the time. However, they all have highly sub-optimal worst case pe ...
Chapter 11: Indexing and Hashing
... In both leaf and internal nodes, we cannot guarantee that K1 < K2 < K3 < . . . < Kn–1 but can guarantee K1 ≤ K2 ≤ K3 ≤ . . . ≤ Kn–1 Search-keys in the subtree to which Pi points are ≤ Ki,, but not necessarily < Ki, To see why, suppose same search key value V is present in two leaf node Li an ...
... In both leaf and internal nodes, we cannot guarantee that K1 < K2 < K3 < . . . < Kn–1 but can guarantee K1 ≤ K2 ≤ K3 ≤ . . . ≤ Kn–1 Search-keys in the subtree to which Pi points are ≤ Ki,, but not necessarily < Ki, To see why, suppose same search key value V is present in two leaf node Li an ...
Lock-free internal binary search trees with memory management
... versions protecting the data structure via mutual exclusion. Unfortunately, non-blocking algorithms have their own set of associated problems. The complexity of their design means that even minor improvements to existing algorithms warrant publication as an academic paper accompanied with a detailed ...
... versions protecting the data structure via mutual exclusion. Unfortunately, non-blocking algorithms have their own set of associated problems. The complexity of their design means that even minor improvements to existing algorithms warrant publication as an academic paper accompanied with a detailed ...
Linked lists
... Insert and remove can be expensive (a lot of copies) if we don’t want to leave holes in the middle of the array. Continuous memory for easy index Dynamic arrays Limitations: Capacity is dynamic, memory still may not be fully utilized, but better than static arrays. Insert and remove can ...
... Insert and remove can be expensive (a lot of copies) if we don’t want to leave holes in the middle of the array. Continuous memory for easy index Dynamic arrays Limitations: Capacity is dynamic, memory still may not be fully utilized, but better than static arrays. Insert and remove can ...
A Fully Retroactive Priority Queues
... Naturally, we cannot hope to directly update this picture each time our priority queue changes and hope to retain efficient performance. A long cascade of this sort will incur a linear-cost update: much too expensive. Fortunately, in the partially retroactive case, we only need to be concerned with ...
... Naturally, we cannot hope to directly update this picture each time our priority queue changes and hope to retain efficient performance. A long cascade of this sort will incur a linear-cost update: much too expensive. Fortunately, in the partially retroactive case, we only need to be concerned with ...
Unit 7 Powerpoint Presentation
... which elements may be deleted at one end called the “TOP” of stack. -- A stack is a last-in-first-out ( LIFO ) structure. -- Insertion operation is referred as “PUSH” and deletion operation is referred as “POP”. -- The most accessible element in the stack is the element at the position “TOP”. -- Sta ...
... which elements may be deleted at one end called the “TOP” of stack. -- A stack is a last-in-first-out ( LIFO ) structure. -- Insertion operation is referred as “PUSH” and deletion operation is referred as “POP”. -- The most accessible element in the stack is the element at the position “TOP”. -- Sta ...
Scalable Address Spaces Using RCU Balanced Trees
... with RCU, and none of the balanced trees in the Linux kernel use RCU. The B ONSAI tree introduced by this paper is one solution to applying RCU to complicated data structures. Trees with lock-free lookup. Fraser [6, 7] introduced a clever design for a red-black tree that allows read operations to pr ...
... with RCU, and none of the balanced trees in the Linux kernel use RCU. The B ONSAI tree introduced by this paper is one solution to applying RCU to complicated data structures. Trees with lock-free lookup. Fraser [6, 7] introduced a clever design for a red-black tree that allows read operations to pr ...
I n - Virginia Tech
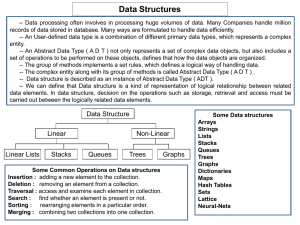
... • Are all data inserted into the data structure at the beginning, or are insertions interspersed with other operations? • Can data be deleted? • Are all data processed in some welldefined order, or is random access allowed? ...
... • Are all data inserted into the data structure at the beginning, or are insertions interspersed with other operations? • Can data be deleted? • Are all data processed in some welldefined order, or is random access allowed? ...