treelib Documentation
... object. In this manner, the traversing will not continue to following children of node whose condition does not pass the filter. key, reverse are present to sort :class:Node objects at the same level. tree.filter_nodes(func) Filters all nodes by function. func is passed one node as an argument and t ...
... object. In this manner, the traversing will not continue to following children of node whose condition does not pass the filter. key, reverse are present to sort :class:Node objects at the same level. tree.filter_nodes(func) Filters all nodes by function. func is passed one node as an argument and t ...
Dynamic Optimality—Almost ∗ Erik D. Demaine Dion Harmon
... lower bound. This lower bound considers applying the access sequence to a fixed lower-bound tree which, in our case, is a perfect binary tree P . The bound counts the number of “interleaves”, i.e., switches from accessing the left subtree of a node to accessing the right subtree of a node, or vice v ...
... lower bound. This lower bound considers applying the access sequence to a fixed lower-bound tree which, in our case, is a perfect binary tree P . The bound counts the number of “interleaves”, i.e., switches from accessing the left subtree of a node to accessing the right subtree of a node, or vice v ...
File - Prof H.M.Patel
... Creating a node means defining its structure, allocating memory to it and its initialization. As discussed earlier, the node of a linked list consists of data and a pointer to next node. To define a node containing an integer data and a pointer to next node in C language, we can use a self-ref ...
... Creating a node means defining its structure, allocating memory to it and its initialization. As discussed earlier, the node of a linked list consists of data and a pointer to next node. To define a node containing an integer data and a pointer to next node in C language, we can use a self-ref ...
Model Viva Questions for “Name of the Lab: Data structure lab”
... A2 The answer is the void pointer. The heterogeneous linked list contains different data types in it's nodes and we need a link, pointer, to connect them. Since we can't use ordinary pointers for this, we use the void pointer. Void pointer is a generic pointer type, and capable of storing pointer to ...
... A2 The answer is the void pointer. The heterogeneous linked list contains different data types in it's nodes and we need a link, pointer, to connect them. Since we can't use ordinary pointers for this, we use the void pointer. Void pointer is a generic pointer type, and capable of storing pointer to ...
Dijkstra`s Algorithm
... which support a collection of algorithms. The amortized analysis is the only way in which the fancier data structure can be proved better than the standard binary heap data structure. Lower Bounds and NP-Completeness Most of the time we will do worst case analysis in this course. This gives us an up ...
... which support a collection of algorithms. The amortized analysis is the only way in which the fancier data structure can be proved better than the standard binary heap data structure. Lower Bounds and NP-Completeness Most of the time we will do worst case analysis in this course. This gives us an up ...
lecture_notes
... which support a collection of algorithms. The amortized analysis is the only way in which the fancier data structure can be proved better than the standard binary heap data structure. Lower Bounds and NP-Completeness Most of the time we will do worst case analysis in this course. This gives us an up ...
... which support a collection of algorithms. The amortized analysis is the only way in which the fancier data structure can be proved better than the standard binary heap data structure. Lower Bounds and NP-Completeness Most of the time we will do worst case analysis in this course. This gives us an up ...
Doubly linked lists 1 - Richard Kay`s BCU/CEBE Page
... a large movement of data which will slow the operation of the program. These problems can be alleviated by using 'dynamic data structures and storing their locations in an array. The problem of determining the maximum size of the pointer array is still present but this will be considerably less than ...
... a large movement of data which will slow the operation of the program. These problems can be alleviated by using 'dynamic data structures and storing their locations in an array. The problem of determining the maximum size of the pointer array is still present but this will be considerably less than ...
Study and Optimization of T-tree Index in Main Memory Database
... TTB-tree can quickly find its successor nodes by the successor pointer and can effectively solve the problem of data overflow. TTB-tree algorithms of searching and inserting and deleting are similar with the T-tree operation algorithms .The difference is that: in the insertion operation ,when need t ...
... TTB-tree can quickly find its successor nodes by the successor pointer and can effectively solve the problem of data overflow. TTB-tree algorithms of searching and inserting and deleting are similar with the T-tree operation algorithms .The difference is that: in the insertion operation ,when need t ...
PPT - WSU EECS - Washington State University
... from a stack only at the top. For this reason, a stack is referred to as a last-in, first-out (LIFO) data structure. A stack is referenced via a pointer to the top element of the stack. The link member in the last node of the stack is set to NULL to indicate the bottom of the stack. ...
... from a stack only at the top. For this reason, a stack is referred to as a last-in, first-out (LIFO) data structure. A stack is referenced via a pointer to the top element of the stack. The link member in the last node of the stack is set to NULL to indicate the bottom of the stack. ...
Review of Elementary Data Structures
... What is data structure? In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently. A data structure is a way of organizing data that considers not only the items stored, but also their relationship to each other. Advanc ...
... What is data structure? In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently. A data structure is a way of organizing data that considers not only the items stored, but also their relationship to each other. Advanc ...
2-3-4 Trees - Randomly Philled
... comparable to the amount of unused space (you get a little better performance with 2-3-4 than the balancing trees with a relative price in data storage) • Why not use a linked list instead of an array? There is an increased amount of overhead with doing that as well, but if that is necessary to reli ...
... comparable to the amount of unused space (you get a little better performance with 2-3-4 than the balancing trees with a relative price in data storage) • Why not use a linked list instead of an array? There is an increased amount of overhead with doing that as well, but if that is necessary to reli ...
lecture12
... organized into some data structure that provides efficient operations for search (and for insert, because insert is used to fill the data structure) CS 103 ...
... organized into some data structure that provides efficient operations for search (and for insert, because insert is used to fill the data structure) CS 103 ...
Data Structures and Other Objects Using C++
... Find the item. If the item has a right child, rearrange the tree: Find smallest item in the right subtree Copy that smallest item onto the one that you want to remove Remove the extra copy of the smallest item (making sure that you keep the tree connected) ...
... Find the item. If the item has a right child, rearrange the tree: Find smallest item in the right subtree Copy that smallest item onto the one that you want to remove Remove the extra copy of the smallest item (making sure that you keep the tree connected) ...
Data Structures and Other Objects Using C++
... Find the item. If the item has a right child, rearrange the tree: Find smallest item in the right subtree Copy that smallest item onto the one that you want to remove Remove the extra copy of the smallest item (making sure that you keep the tree connected) ...
... Find the item. If the item has a right child, rearrange the tree: Find smallest item in the right subtree Copy that smallest item onto the one that you want to remove Remove the extra copy of the smallest item (making sure that you keep the tree connected) ...
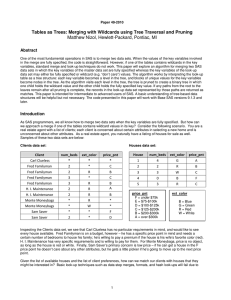
Tables As Trees: Merging with Wildcards Using Tree Traversal and Pruning
... That the key variables are all the same length (even if that length exceeds the required storage for shorter variables) ...
... That the key variables are all the same length (even if that length exceeds the required storage for shorter variables) ...
Arrays and Linked Lists
... { link v to its predecessor } { link v to its successor } { link p’s old successor to v } {link p to its new successor, v } {the position for the element e } ...
... { link v to its predecessor } { link v to its successor } { link p’s old successor to v } {link p to its new successor, v } {the position for the element e } ...