Data Structures in Java
... • Read left child, then parent, then right child • Essentially scans whole tree from left to right • inorder(node x) inorder(x.left) print(x) inorder(x.right) ...
... • Read left child, then parent, then right child • Essentially scans whole tree from left to right • inorder(node x) inorder(x.left) print(x) inorder(x.right) ...
Lecture 3: Red-black trees. Augmenting data structures
... Lecture 3: Red-black trees. Augmenting data structures A red-black tree is a binary search tree with the following properties: 1. Every node is either red or black. 2. The root is black. 3. Every leaf (NIL) is black. 4. If a node is red, then both its children are black. Hence there cannot be two co ...
... Lecture 3: Red-black trees. Augmenting data structures A red-black tree is a binary search tree with the following properties: 1. Every node is either red or black. 2. The root is black. 3. Every leaf (NIL) is black. 4. If a node is red, then both its children are black. Hence there cannot be two co ...
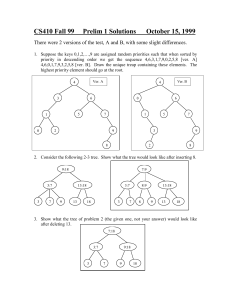
Prelim 1 solutions - Cornell Computer Science
... follow the path up to the root from the inserted or deleted leaf and add or subtract one at each node. This takes only O(log n) extra time. On a split or join in a 2-3 tree or a rotate in a red-black tree, the new counts of the affected nodes can be computed locally in O(1) time from the counts of t ...
... follow the path up to the root from the inserted or deleted leaf and add or subtract one at each node. This takes only O(log n) extra time. On a split or join in a 2-3 tree or a rotate in a red-black tree, the new counts of the affected nodes can be computed locally in O(1) time from the counts of t ...
Chapter 10
... necessary by swapping with its parent until it is not less than its parent See Figures 10.17 and 10.18 To delete a node from a heap, replace it with the last node on the bottom level and bubble that node up or down as necessary See Figures 10.19 and 10.20 ...
... necessary by swapping with its parent until it is not less than its parent See Figures 10.17 and 10.18 To delete a node from a heap, replace it with the last node on the bottom level and bubble that node up or down as necessary See Figures 10.19 and 10.20 ...
7 Data Structures – Binary Search Trees
... – If the tree is a linear chain of n nodes, however, the same operations take (n) worst-case time. ...
... – If the tree is a linear chain of n nodes, however, the same operations take (n) worst-case time. ...
Binary Search Trees
... – If the tree is a linear chain of n nodes, however, the same operations take (n) worst-case time. ...
... – If the tree is a linear chain of n nodes, however, the same operations take (n) worst-case time. ...
Data Structures and Search Algorithms
... Almost like linked lists! Traverse: Pre-order v. Post-order v. Inorder Node, edge, sibling/parent/child, leaf ...
... Almost like linked lists! Traverse: Pre-order v. Post-order v. Inorder Node, edge, sibling/parent/child, leaf ...
Problem 7—Skewed Trees Trees are particularly annoying to test
... substandard and cannot be guaranteed to avoid the greenery. Hal is not actually afraid of trees—he was evidently born without fear and could never be called “yellow”—but they are annoying. Hal's spent enough time observing trees to notice that some are more even than others. Some have branches evenl ...
... substandard and cannot be guaranteed to avoid the greenery. Hal is not actually afraid of trees—he was evidently born without fear and could never be called “yellow”—but they are annoying. Hal's spent enough time observing trees to notice that some are more even than others. Some have branches evenl ...
Augmenting Data Structures 2
... Maintain a dynamic set of elements with each element x containing an interval int[x] Support the following operations: • INSERT(T,x) : Adds an element x whose int field contains an interval to the tree • DELETE(T,x): Removes the element x from the tree T • SEARCH(T,i): Returns a pointer to an el ...
... Maintain a dynamic set of elements with each element x containing an interval int[x] Support the following operations: • INSERT(T,x) : Adds an element x whose int field contains an interval to the tree • DELETE(T,x): Removes the element x from the tree T • SEARCH(T,i): Returns a pointer to an el ...
Binary Trees: Notes on binary trees
... levels are full with exception to the last level and it is filled from left to right. A full binary tree is one where if a node has a child, then it has two children. ...
... levels are full with exception to the last level and it is filled from left to right. A full binary tree is one where if a node has a child, then it has two children. ...
1 Balanced Binary Search Trees
... Note that inserts happen only at a new leaf. Also an insertion may create an imbalance only at the vertices in the path from the new leaf to the root and nowhere else. The local operation which are used to maintain balance after insertion and deletion is rotation. This operation moves the nodes arou ...
... Note that inserts happen only at a new leaf. Also an insertion may create an imbalance only at the vertices in the path from the new leaf to the root and nowhere else. The local operation which are used to maintain balance after insertion and deletion is rotation. This operation moves the nodes arou ...