Lecture 20 Student Notes
... In order for Delete to work correctly, we must augment our Euler-Tour trees. First, each EulerTour tree must keep track of its subtree sizes in order to find which of |Tv | and |Tu | is smaller in O(1). (This augmentation is standard and easy.) We also need to augment our trees to know for each node ...
... In order for Delete to work correctly, we must augment our Euler-Tour trees. First, each EulerTour tree must keep track of its subtree sizes in order to find which of |Tv | and |Tu | is smaller in O(1). (This augmentation is standard and easy.) We also need to augment our trees to know for each node ...
Time and location: Materials covered concepts (so far) in a nutshell COS 226
... Resizable array questions • resizing array by one gives amortized linear time per item (bad) • resizing array by doubling/halving gives amortized constant time (good) • What if instead of doubling the size of the array, we triple the size? good or bad? • Resizing also includes shrinking the array by ...
... Resizable array questions • resizing array by one gives amortized linear time per item (bad) • resizing array by doubling/halving gives amortized constant time (good) • What if instead of doubling the size of the array, we triple the size? good or bad? • Resizing also includes shrinking the array by ...
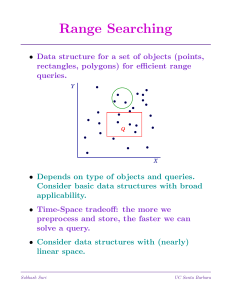
Range Searching
... then read off points until yhi reached. • Since each set is searched for the same key, ylo, we can improve the search to O(1) per set. • In effect, we do the first search in O(log n) time, but then use that information to search other structures more efficiently. • The key is to place smart hooks li ...
... then read off points until yhi reached. • Since each set is searched for the same key, ylo, we can improve the search to O(1) per set. • In effect, we do the first search in O(log n) time, but then use that information to search other structures more efficiently. • The key is to place smart hooks li ...
Sandhya Dasu
... • Delete(i) – After updating a counter’s value it, this operation is performed to indicate that its value is now below T » Contd… ...
... • Delete(i) – After updating a counter’s value it, this operation is performed to indicate that its value is now below T » Contd… ...
Path Queries on Compressed XML
... structures in a large document are likely to be repeated many times. If one considers an example of extreme regularity, that of an XML-encoded relational table with R rows and C columns, the skeleton has size O(CxR), and the compressed skeleton as in Figure (b) has size O(C + R). This is further red ...
... structures in a large document are likely to be repeated many times. If one considers an example of extreme regularity, that of an XML-encoded relational table with R rows and C columns, the skeleton has size O(CxR), and the compressed skeleton as in Figure (b) has size O(C + R). This is further red ...
Quiz 4 Solutions
... Q19: Which of the following statements about stacks is incorrect? a. Stacks can be implemented using linked lists. b. Stacks are first-in, first-out (FIFO) data structures. c. New nodes can only be added to the top of the stack. d. The last node (at the bottom) of a stack has a null (0) link. ANS b. ...
... Q19: Which of the following statements about stacks is incorrect? a. Stacks can be implemented using linked lists. b. Stacks are first-in, first-out (FIFO) data structures. c. New nodes can only be added to the top of the stack. d. The last node (at the bottom) of a stack has a null (0) link. ANS b. ...
Lecture 9 — 16 Feb, 2012 1 Overview 2 The problem
... • insert(x) or delete(x): Same as inserting or deleting in each of the hash tables. For each hash table, deletion is O(1) and insertion is O(1) expected amortised. So total expected amortised time is O(log u). • succ(x) or pred(x): We do a nested binary search to find the longest common subsequence ...
... • insert(x) or delete(x): Same as inserting or deleting in each of the hash tables. For each hash table, deletion is O(1) and insertion is O(1) expected amortised. So total expected amortised time is O(log u). • succ(x) or pred(x): We do a nested binary search to find the longest common subsequence ...
Selection and Search
... ● Here’s another function that does the same: TreeSearch(x, k) while (x != NULL and if (k < key[x]) x = left[x]; else x = right[x]; return x; ...
... ● Here’s another function that does the same: TreeSearch(x, k) while (x != NULL and if (k < key[x]) x = left[x]; else x = right[x]; return x; ...
Constructing the Suffix Tree of a Tree with a Large Alphabet
... of these procedures can be performed in a linear time. We then construct the suffix tree TU 0 of U 0 by using our entire algorithm recursively. After that, we construct Tsmall from TU 0 as follows. We can consider a tree T 0 whose edge labels of TU 0 are modified to the original labels in U : for examp ...
... of these procedures can be performed in a linear time. We then construct the suffix tree TU 0 of U 0 by using our entire algorithm recursively. After that, we construct Tsmall from TU 0 as follows. We can consider a tree T 0 whose edge labels of TU 0 are modified to the original labels in U : for examp ...
Balanced BSTs
... • Every node is red or black • The root is black • Leaves are nil nodes that are black • If a node is red then both its children are black • For each node, all simple paths from the node to descendant leaves contain the same number of black nodes ...
... • Every node is red or black • The root is black • Leaves are nil nodes that are black • If a node is red then both its children are black • For each node, all simple paths from the node to descendant leaves contain the same number of black nodes ...
Heap Sort - Priority Queues
... A possible problem: an estimate of the maximum heap size is required in advance (but normally we can resize if needed) Note: we will draw the heaps as trees, with the implication that an actual implementation will use simple arrays Side notes: it’s not wise to store normal binary trees in arrays, be ...
... A possible problem: an estimate of the maximum heap size is required in advance (but normally we can resize if needed) Note: we will draw the heaps as trees, with the implication that an actual implementation will use simple arrays Side notes: it’s not wise to store normal binary trees in arrays, be ...
Cache-sensitive Memory Layout for Binary Trees.
... root of the TLB-sized subtree is not of course the only problematic node, but the problem is most pronounced at the root.) The problem can be fixed by noting that we can freely reorder the cache blocks inside a TLB page. The Bl -sized TLB page consists of Bl /Bl−1 cache blocks, and the subtree locat ...
... root of the TLB-sized subtree is not of course the only problematic node, but the problem is most pronounced at the root.) The problem can be fixed by noting that we can freely reorder the cache blocks inside a TLB page. The Bl -sized TLB page consists of Bl /Bl−1 cache blocks, and the subtree locat ...
Lecture6MRM
... Then the representation invariant will always be true at the completion of each method. Assuming the code is not concurrent! ...
... Then the representation invariant will always be true at the completion of each method. Assuming the code is not concurrent! ...
Intelligent Agents and Applications in Enterprise Computing
... interpretation by subject matter experts, and staff turnover place a significant burden on corporations . seeking to uttlize the latest technologies. All of these problems can be expected to increase. ...
... interpretation by subject matter experts, and staff turnover place a significant burden on corporations . seeking to uttlize the latest technologies. All of these problems can be expected to increase. ...
Range Queries in Non-blocking k
... Brown and Helga [9] presented a k-ST in which each internal node has k children, and each leaf contains up to k − 1 keys. For large values of k, this translates into an algorithm which minimizes cache misses and benefits from processor pre-fetching mechanisms. In some ways, the k-ST is similar to a ...
... Brown and Helga [9] presented a k-ST in which each internal node has k children, and each leaf contains up to k − 1 keys. For large values of k, this translates into an algorithm which minimizes cache misses and benefits from processor pre-fetching mechanisms. In some ways, the k-ST is similar to a ...
Binary search tree
In computer science, binary search trees (BST), sometimes called ordered or sorted binary trees, are a particular type of containers: data structures that store ""items"" (such as numbers, names and etc.) in memory. They allow fast lookup, addition and removal of items, and can be used to implement either dynamic sets of items, or lookup tables that allow finding an item by its key (e.g., finding the phone number of a person by name).Binary search trees keep their keys in sorted order, so that lookup and other operations can use the principle of binary search: when looking for a key in a tree (or a place to insert a new key), they traverse the tree from root to leaf, making comparisons to keys stored in the nodes of the tree and deciding, based on the comparison, to continue searching in the left or right subtrees. On average, this means that each comparison allows the operations to skip about half of the tree, so that each lookup, insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree. This is much better than the linear time required to find items by key in an (unsorted) array, but slower than the corresponding operations on hash tables.They are a special case of the more general B-tree with order equal to two.