Tutorial 1 C++ Programming
... • What is the time complexity of f(n), if g(n) is: To answer this, we must draw the recursive execution tree… a) g(n) = O(1) O(n), a sum of geometric series of 1+2+4+…+2log2 n = 1+2+4+…+n = c*n b) g(n) = O(n) O(n log n), a sum of (n+n+n+…+n) log2 n times, so, n log n c) g(n) = O(n2) O(n2), a sum of ...
... • What is the time complexity of f(n), if g(n) is: To answer this, we must draw the recursive execution tree… a) g(n) = O(1) O(n), a sum of geometric series of 1+2+4+…+2log2 n = 1+2+4+…+n = c*n b) g(n) = O(n) O(n log n), a sum of (n+n+n+…+n) log2 n times, so, n log n c) g(n) = O(n2) O(n2), a sum of ...
python-example
... formatting as specified in the problem That’s only fair in comparing Python with ...
... formatting as specified in the problem That’s only fair in comparing Python with ...
Algorithms Lecture 5 Name:___________________________
... a.) Why was recursive fibonacci so slow? ...
... a.) Why was recursive fibonacci so slow? ...
Week 6 Precept COS 226 Data Structures and Algorithms Computer Science Department
... tree after inserting key H and then draw it again after inserting key T. The new tree must be a valid red-black tree. ...
... tree after inserting key H and then draw it again after inserting key T. The new tree must be a valid red-black tree. ...
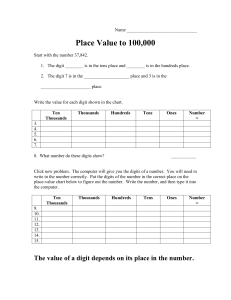
Place Value game
... 1. The digit ________ is in the tens place and ________ is in the hundreds place. 2. The digit 7 is in the ____________________ place and 3 is in the ______________________ place. ...
... 1. The digit ________ is in the tens place and ________ is in the hundreds place. 2. The digit 7 is in the ____________________ place and 3 is in the ______________________ place. ...
Analysis of Algorithms
... log2n! for any comparison-based sorting algorithm, since the longest path represents the worst case and its length is the height log2n! n log2n (by Sterling approximation) This lower bound is tight (mergesort or heapsort) Ex. Prove that 5 (or 7) comparisons are necessary and sufficient for sor ...
... log2n! for any comparison-based sorting algorithm, since the longest path represents the worst case and its length is the height log2n! n log2n (by Sterling approximation) This lower bound is tight (mergesort or heapsort) Ex. Prove that 5 (or 7) comparisons are necessary and sufficient for sor ...