Sample Chapter
... ensure that it does not have any conflict with the existing rules. Besides this, there may be more than one number of rules that can be applied (typically called fired) in one situation. While choosing the rule also, the conflict should not happen. If conflict is found, it should be resolved in foll ...
... ensure that it does not have any conflict with the existing rules. Besides this, there may be more than one number of rules that can be applied (typically called fired) in one situation. While choosing the rule also, the conflict should not happen. If conflict is found, it should be resolved in foll ...
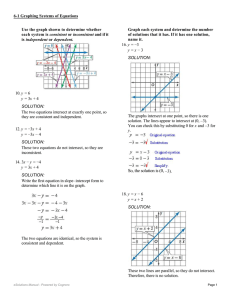
So, the solution is (0, –3).
... d. The domain of each of these equations is the set of real numbers greater than or equal to 0. The range of each of these equations is the set of real numbers greater than or equal to 0. Graph each system and determine the number of solutions that it has. If it has one solution, name it. ...
... d. The domain of each of these equations is the set of real numbers greater than or equal to 0. The range of each of these equations is the set of real numbers greater than or equal to 0. Graph each system and determine the number of solutions that it has. If it has one solution, name it. ...
Chap 1.I.1 - Gauss`s Method
... system where back-substitution can be used to find the solutions(s) to the original linear system. The form of the linear system we obtain is given a particular name. Echelon Form In a row of a linear system, the first variable with a nonzero coefficient is called the row’s leading variable. A syste ...
... system where back-substitution can be used to find the solutions(s) to the original linear system. The form of the linear system we obtain is given a particular name. Echelon Form In a row of a linear system, the first variable with a nonzero coefficient is called the row’s leading variable. A syste ...
Toward General Analysis of Recursive Probability Models
... defined recursively, and is calculated directly from the sub-expressions from which the newly created expression is derived. For a variable, its level is the number denoting the variable. For a A.-abstraction, the level is derived from the level of the expression in the body of the abstraction, but ...
... defined recursively, and is calculated directly from the sub-expressions from which the newly created expression is derived. For a variable, its level is the number denoting the variable. For a A.-abstraction, the level is derived from the level of the expression in the body of the abstraction, but ...
Lecture 05 Part A - First Order Logic (FOL)
... Last unification fails: only because x can’t take values John and Bill at the same time Problem is due to use of same variable x in both sentences Simple solution: Standardizing apart eliminates overlap of variables, e.g., Knows(z, Bill) ...
... Last unification fails: only because x can’t take values John and Bill at the same time Problem is due to use of same variable x in both sentences Simple solution: Standardizing apart eliminates overlap of variables, e.g., Knows(z, Bill) ...
Elimination Proof Method - Student AND Teacher
... We will now add the two new equations together. Why are we allowed to do this? This step requires us to use the Addition Property of Equality AND the Substitution Property simultaneously as we add the lefthand sides of the equations together and the right-hand sides of the equations together. We are ...
... We will now add the two new equations together. Why are we allowed to do this? This step requires us to use the Addition Property of Equality AND the Substitution Property simultaneously as we add the lefthand sides of the equations together and the right-hand sides of the equations together. We are ...
1. Procedural knowledge Vs Declarative Knowledge - E
... Example 1: It is easier to drive from an unfamiliar place from home, rather than from home to an unfamiliar place. If you consider a home as starting place an unfamiliar as goal then we have to back track from unfamiliar place to home. Example 2: Consider a problem of symbolic integration. The probl ...
... Example 1: It is easier to drive from an unfamiliar place from home, rather than from home to an unfamiliar place. If you consider a home as starting place an unfamiliar as goal then we have to back track from unfamiliar place to home. Example 2: Consider a problem of symbolic integration. The probl ...