Compact stars with a small electric charge: the limiting radius to
... particles that make the bulk of dark matter should be neutral, one possible candidate is the neutralino [39], however, some of these particles could be electrically charged. The mass m to charge q ratio of these supersymmetric particles are much higher than the baryonic mass to charge ratio, indeed ...
... particles that make the bulk of dark matter should be neutral, one possible candidate is the neutralino [39], however, some of these particles could be electrically charged. The mass m to charge q ratio of these supersymmetric particles are much higher than the baryonic mass to charge ratio, indeed ...
11-3 Solving Equations with Variables on Both Sides
... variables on both sides of the equal sign. Solving an equation with variables on both sides is similar to solving an equation with a variable on only one side. You can add or subtract a term containing a variable on both sides of an equation. ...
... variables on both sides of the equal sign. Solving an equation with variables on both sides is similar to solving an equation with a variable on only one side. You can add or subtract a term containing a variable on both sides of an equation. ...
Externally fed accretion on to protostars
... the gravitational force from the protostar and that from interior cloud gas. Our problem is thus identical to the classic inflow calculation of Bondi (1952), except that we include self-gravity of the gas. Like Bondi, we apply the inner boundary condition that this material is in free fall on to the ...
... the gravitational force from the protostar and that from interior cloud gas. Our problem is thus identical to the classic inflow calculation of Bondi (1952), except that we include self-gravity of the gas. Like Bondi, we apply the inner boundary condition that this material is in free fall on to the ...
Chapter 10 Time-Varying Fields and Maxwell`s Equations
... The basic relationships of the electrostatic and the steady magnetic field were obtained in the previous nine chapters, and we are now ready to discuss timevarying fields. The discussion will be short, for vector analysis and vector calculus should now be more familiar tools; some of the relationshi ...
... The basic relationships of the electrostatic and the steady magnetic field were obtained in the previous nine chapters, and we are now ready to discuss timevarying fields. The discussion will be short, for vector analysis and vector calculus should now be more familiar tools; some of the relationshi ...
The Murad-Brandenburg Poynting Field Conservation Equation and
... derivation also reveals that you can have a Poynting vector purely with situations where only an electric or magnetic field exists as separate entities if there are no currents as seen by the second equation. Using Maxwell’s equations can produce terms that are purely due to the magnetic field or el ...
... derivation also reveals that you can have a Poynting vector purely with situations where only an electric or magnetic field exists as separate entities if there are no currents as seen by the second equation. Using Maxwell’s equations can produce terms that are purely due to the magnetic field or el ...
Transport Equations for Semiconductors
... The modern computer and telecommunication industry relies heavily on the use and development of semiconductor devices. The first semiconductor device (a germanium transistor) has been built in 1947 by Bardeen, Brattain and Shockley, who have been awarded the Nobel prize in 1956. In the following dec ...
... The modern computer and telecommunication industry relies heavily on the use and development of semiconductor devices. The first semiconductor device (a germanium transistor) has been built in 1947 by Bardeen, Brattain and Shockley, who have been awarded the Nobel prize in 1956. In the following dec ...
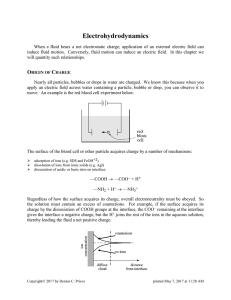
Electrohydrodynamics
... Instead of using thermodynamics, Boltzmann’s equation can also be obtained by integrating the transport equations. Knowing that the solution next to the charged surface is nonuniform in concentration owing to an electric field normal to the surface, we can express the net flux of ions toward the sur ...
... Instead of using thermodynamics, Boltzmann’s equation can also be obtained by integrating the transport equations. Knowing that the solution next to the charged surface is nonuniform in concentration owing to an electric field normal to the surface, we can express the net flux of ions toward the sur ...
excitation of breather (bion) in superlattice
... be interpreted as bound states of solitons and antisolitons.The solution of sG equation has deeply influenced our understanding of various condensed matter phenomena, notably among which are the charge transfers in quasi 1-D conductors [13,14], flow of flux quanta in Josephson junction [15] and in ...
... be interpreted as bound states of solitons and antisolitons.The solution of sG equation has deeply influenced our understanding of various condensed matter phenomena, notably among which are the charge transfers in quasi 1-D conductors [13,14], flow of flux quanta in Josephson junction [15] and in ...