Solve Rational Equations
... 5: Remove any factors equal to 1, and write the result in simpli…ed form. 6: Solve the resulting equation. 7: Check all possible solutions in the original equation. Example 1: (Solving rational expressions) Solve the following equations. ...
... 5: Remove any factors equal to 1, and write the result in simpli…ed form. 6: Solve the resulting equation. 7: Check all possible solutions in the original equation. Example 1: (Solving rational expressions) Solve the following equations. ...
AP Calculus AB 2014
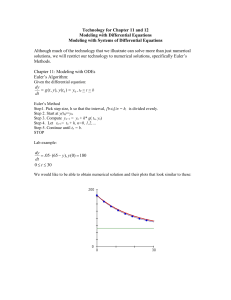
... separable differential equations analytically, and solve differential equations using numerical techniques such as Euler’s method. ...
... separable differential equations analytically, and solve differential equations using numerical techniques such as Euler’s method. ...
PowerPoint 1
... A linear equation in one variable is an equation that can be written in the form ax = b where a and b are constants and a 0. A number is a solution of an equation if the statement is true when the number is substituted for the variable. Two equations are equivalent if they have the same solutions. ...
... A linear equation in one variable is an equation that can be written in the form ax = b where a and b are constants and a 0. A number is a solution of an equation if the statement is true when the number is substituted for the variable. Two equations are equivalent if they have the same solutions. ...
Lecture 3: We began the study of the Simplex Method for solving
... If we try to increase x3 to improve the objective function value then, the first equation and the nonnegativity of x4 us that we can increase it to at most 5, the second constraint tells ...
... If we try to increase x3 to improve the objective function value then, the first equation and the nonnegativity of x4 us that we can increase it to at most 5, the second constraint tells ...