Quantum theory of many − particle systems
... This is the Lagrange equation for a particle in one dimension. We have derived it for a very simple mechanical problem, but the result can be generalized to any number of particles and any number of dimensions. If we consider a system of N particles in three dimensions, we need 3N coordinates to spe ...
... This is the Lagrange equation for a particle in one dimension. We have derived it for a very simple mechanical problem, but the result can be generalized to any number of particles and any number of dimensions. If we consider a system of N particles in three dimensions, we need 3N coordinates to spe ...
Deriving new operator identities by alternately using normally
... rules to Dirac’s ket-bra projectors in previous work. In this work, by alternately using the technique of integration within normal, antinormal, and Weyl ordering of operators we not only derive some new operator ordering identities, but also deduce some new integration formulas regarding Laguerre a ...
... rules to Dirac’s ket-bra projectors in previous work. In this work, by alternately using the technique of integration within normal, antinormal, and Weyl ordering of operators we not only derive some new operator ordering identities, but also deduce some new integration formulas regarding Laguerre a ...
2.3 SS - LSU Mathematics
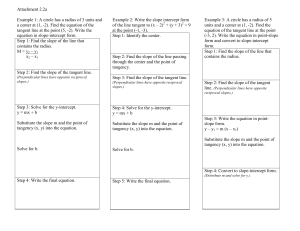
... 1. Determining the Slope of a Line 2. Sketching a Line Given a Point and the Slope 3. Finding the Equation of a Line Using the Point-Slope Form 4. Finding the Equation of a Line Using the Slope-Intercept Form 5. Writing the Equation of a Line in Standard Form 6. Finding the Slope and the y-intercept ...
... 1. Determining the Slope of a Line 2. Sketching a Line Given a Point and the Slope 3. Finding the Equation of a Line Using the Point-Slope Form 4. Finding the Equation of a Line Using the Slope-Intercept Form 5. Writing the Equation of a Line in Standard Form 6. Finding the Slope and the y-intercept ...
Mass Relationships of Atoms
... 3. Use the coefficients in the balanced equation to relate the number of moles of known substances to the unknown one. 4. Convert to desired units (g, L, etc.). ...
... 3. Use the coefficients in the balanced equation to relate the number of moles of known substances to the unknown one. 4. Convert to desired units (g, L, etc.). ...