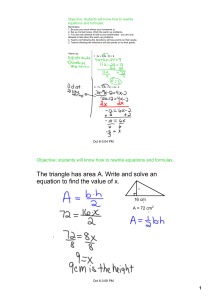
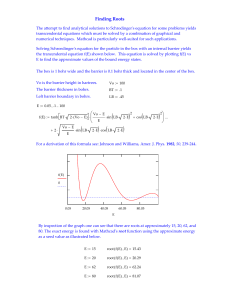
Let`s review recursive formulas.
... Define the variables and write an exponential equation that models this growth. Choose two table points and see if it works. ...
... Define the variables and write an exponential equation that models this growth. Choose two table points and see if it works. ...