Panel Data - University of Vaasa
... parameters from the first-differenced equation with OLS are called the first-differenced estimators (FD estimators). We will deal with other fixed effect estimators later. In summary: Differencing eliminates all unobserved time invariant factors from the model. A major pitfall is that differencing a ...
... parameters from the first-differenced equation with OLS are called the first-differenced estimators (FD estimators). We will deal with other fixed effect estimators later. In summary: Differencing eliminates all unobserved time invariant factors from the model. A major pitfall is that differencing a ...
Simplex algorithm for problems with bounded variables
... We find similar values as in problems where there are no upper bounds, except for non basic variables x j = 0 or u j j ∈ JB ...
... We find similar values as in problems where there are no upper bounds, except for non basic variables x j = 0 or u j j ∈ JB ...
fuzzy classification models based on tanaka`s fuzzy
... deal with fuzzy uncertainty imbedded in data in different ways. For example, FRC method deals with fuzzy type of uncertainty by modeling the relationship between cluster membership and class membership values. Methods based on fuzzy functions such as FCF and IFCF on the other hand, reflect the fuzzi ...
... deal with fuzzy uncertainty imbedded in data in different ways. For example, FRC method deals with fuzzy type of uncertainty by modeling the relationship between cluster membership and class membership values. Methods based on fuzzy functions such as FCF and IFCF on the other hand, reflect the fuzzi ...
Download File
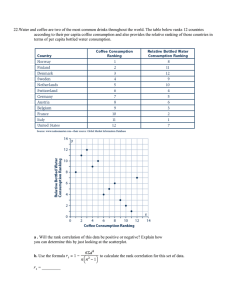
... X with respect to the natural log of its own price. Table 3 shows the regression of the natural log of the quantity demanded of good X with respect to the natural log of its own price and the natural log of the price of the substitute good, Y. Regressions were conducted in Excel. a. Please refer to ...
... X with respect to the natural log of its own price. Table 3 shows the regression of the natural log of the quantity demanded of good X with respect to the natural log of its own price and the natural log of the price of the substitute good, Y. Regressions were conducted in Excel. a. Please refer to ...
Discrete Choice Modeling
... on, for example, how a large a refrigerator a consumer will buy, but not whether they will buy a refrigerator instead of a car (this year), or what brand of refrigerator or car they will choose. Second, the introduction of random elements in models of choice behavior as disturbances, is much less co ...
... on, for example, how a large a refrigerator a consumer will buy, but not whether they will buy a refrigerator instead of a car (this year), or what brand of refrigerator or car they will choose. Second, the introduction of random elements in models of choice behavior as disturbances, is much less co ...
Coefficient of determination
In statistics, the coefficient of determination, denoted R2 or r2 and pronounced R squared, is a number that indicates how well data fit a statistical model – sometimes simply a line or a curve. An R2 of 1 indicates that the regression line perfectly fits the data, while an R2 of 0 indicates that the line does not fit the data at all. This latter can be because the data is utterly non-linear, or because it is random.It is a statistic used in the context of statistical models whose main purpose is either the prediction of future outcomes or the testing of hypotheses, on the basis of other related information. It provides a measure of how well observed outcomes are replicated by the model, as the proportion of total variation of outcomes explained by the model (pp. 187, 287).There are several definitions of R2 that are only sometimes equivalent. One class of such cases includes that of simple linear regression where r2 is used instead of R2. In this case, if an intercept is included, then r2 is simply the square of the sample correlation coefficient (i.e., r) between the outcomes and their predicted values. If additional explanators are included, R2 is the square of the coefficient of multiple correlation. In both such cases, the coefficient of determination ranges from 0 to 1.Important cases where the computational definition of R2 can yield negative values, depending on the definition used, arise where the predictions that are being compared to the corresponding outcomes have not been derived from a model-fitting procedure using those data, and where linear regression is conducted without including an intercept. Additionally, negative values of R2 may occur when fitting non-linear functions to data. In cases where negative values arise, the mean of the data provides a better fit to the outcomes than do the fitted function values, according to this particular criterion.