Lesson 5
... Integers are whole numbers that describe opposite ideas in mathematics. Integers can either be negative(-), positive(+) or zero. The integer zero is neutral. It is neither positive nor negative, but is an integer. Integers can be represented on a number line, which can help us understand the valve o ...
... Integers are whole numbers that describe opposite ideas in mathematics. Integers can either be negative(-), positive(+) or zero. The integer zero is neutral. It is neither positive nor negative, but is an integer. Integers can be represented on a number line, which can help us understand the valve o ...
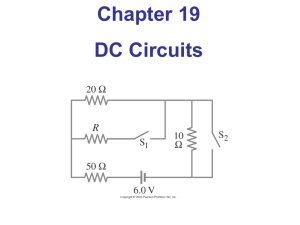
19-3 Kirchhoff`s Rules
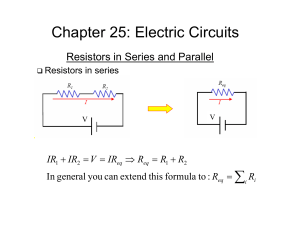
... • Many practical resistor networks cannot be reduced to simple series-parallel combinations (see an example below). • Terminology: -A junction in a circuit is a point where three or more conductors meet. -A loop is any closed conducting path. ...
... • Many practical resistor networks cannot be reduced to simple series-parallel combinations (see an example below). • Terminology: -A junction in a circuit is a point where three or more conductors meet. -A loop is any closed conducting path. ...
Full text
... There are many Fibonacci identities to be found in short informal articles in the early editions of The Fibonacci Quarterly. See, for example, [1] and [2]. The aim of the authors was to gather Fibonacci identities from diverse sources and display them for all to see. Many of the identities that appe ...
... There are many Fibonacci identities to be found in short informal articles in the early editions of The Fibonacci Quarterly. See, for example, [1] and [2]. The aim of the authors was to gather Fibonacci identities from diverse sources and display them for all to see. Many of the identities that appe ...
Math 7 Notes – Unit Three: Applying Rational Numbers Strategy
... 1. The denominator for .71 is 100. The denominator for .127 is 1,000. The least common denominator is 1,000. 2. Add a zero after .71 so it will have a common denominator of 1,000. 3. Add the numerators by adding 710 and 127 = 837. 4. Bring down the common denominator of 1,000. This means there must ...
... 1. The denominator for .71 is 100. The denominator for .127 is 1,000. The least common denominator is 1,000. 2. Add a zero after .71 so it will have a common denominator of 1,000. 3. Add the numerators by adding 710 and 127 = 837. 4. Bring down the common denominator of 1,000. This means there must ...
10419_Honors_Algebra_2_Trigonometry
... handling an accelerated math course who wish to take Calculus in high school to do so if they were not advanced to the geometry level in their freshman year. It also allows students who take Geometry in their freshmen year to take two years of calculus in high school. ...
... handling an accelerated math course who wish to take Calculus in high school to do so if they were not advanced to the geometry level in their freshman year. It also allows students who take Geometry in their freshmen year to take two years of calculus in high school. ...
Day 10: Precious Conjectures Grade 7
... • verify that the conjecture is true for the first ten numbers in the pattern. • select five additional numbers and verify that the conjecture is true for them. These numbers do not have to be consecutive or immediately follow the first ten numbers. • suppose that you were able to write valid statem ...
... • verify that the conjecture is true for the first ten numbers in the pattern. • select five additional numbers and verify that the conjecture is true for them. These numbers do not have to be consecutive or immediately follow the first ten numbers. • suppose that you were able to write valid statem ...
Math 8 (Pre-Algebra) Curriculum Map 2011-2012
... volume, weight, capacity, and time to equivalent measurements within the same system. Description: Note: To prepare students for Algebra I, if you teach conversions as a series of proportions, we also suggest that you teach conversions using dimensional analysis. 8.5.3 Solve problems involving scale ...
... volume, weight, capacity, and time to equivalent measurements within the same system. Description: Note: To prepare students for Algebra I, if you teach conversions as a series of proportions, we also suggest that you teach conversions using dimensional analysis. 8.5.3 Solve problems involving scale ...
Application Note AN-1162 Compensator Design Procedure for Buck Converter with Voltage-Mode Error-Amplifier
... For a general solution for unconditional stability for any type of output capacitors, and a wide range of ESR values, local feedback should be implemented with a type III compensation network. Specially, when F0 FESR type II compensator is not useful and type III compensator must be used. The typi ...
... For a general solution for unconditional stability for any type of output capacitors, and a wide range of ESR values, local feedback should be implemented with a type III compensation network. Specially, when F0 FESR type II compensator is not useful and type III compensator must be used. The typi ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.