Induction
... P (n + 1) for all n. We prove (b) by contradiction. Suppose P (n) is not true for all n ∈ N. Set E = {n | P (n) is false}. Then E = ∅ and is a subset of the natural numbers. By the well-ordering property there is a least such n which we label n0 . Since P (1) is true, n0 > 1. By construction, P (n0 ...
... P (n + 1) for all n. We prove (b) by contradiction. Suppose P (n) is not true for all n ∈ N. Set E = {n | P (n) is false}. Then E = ∅ and is a subset of the natural numbers. By the well-ordering property there is a least such n which we label n0 . Since P (1) is true, n0 > 1. By construction, P (n0 ...
7•2 Lesson 1 Lesson Summary
... arrow at −1 and locating the head of the arrow 4.3 units to the right to arrive at the sum, which is 3.3. To model the difference of two rational numbers on a number line (for example, −5.7 − 3), first rewrite the difference as a sum, −5.7 + (−3), and then follow the steps for locating a sum. Place ...
... arrow at −1 and locating the head of the arrow 4.3 units to the right to arrive at the sum, which is 3.3. To model the difference of two rational numbers on a number line (for example, −5.7 − 3), first rewrite the difference as a sum, −5.7 + (−3), and then follow the steps for locating a sum. Place ...
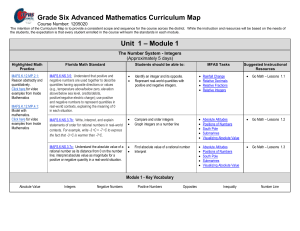
Grade Six Advanced Mathematics Curriculum Map Unit 1 – Module 1
... depending on the purpose at hand, any number in a specified set. ...
... depending on the purpose at hand, any number in a specified set. ...
A Proof Theory for Generic Judgments
... intended as variables to be substituted. This enrichment to proof theory (discussed here in Section 4) holds promise for providing proof systems for the direct reasoning of logic specifications (see, for example, the above mentioned papers as well as [McDowell and Miller 2002; McDowell et al. 2003]) ...
... intended as variables to be substituted. This enrichment to proof theory (discussed here in Section 4) holds promise for providing proof systems for the direct reasoning of logic specifications (see, for example, the above mentioned papers as well as [McDowell and Miller 2002; McDowell et al. 2003]) ...