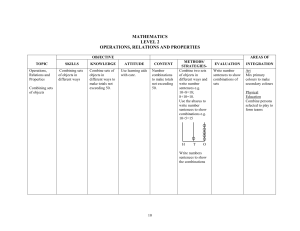
G7-M2 Lesson 4 - Teacher
... What do you think the rules would be for subtracting numbers with same sign? (Do not spend too much time on this question. Allow students to verbally experiment with their responses.) ...
... What do you think the rules would be for subtracting numbers with same sign? (Do not spend too much time on this question. Allow students to verbally experiment with their responses.) ...
Full text
... which is a contradiction, since/? as a divisor of 5 would divide the left-hand side of (12), contrary to the fact that/? is distinct from q, Pi,--,pm. Next, suppose that q\(a-2k -B) or that q\(a + 2k -B). Equation (12) clearly implies in such a case, a = B = l (mod /?). Also if q\a-2k°B^ we must hav ...
... which is a contradiction, since/? as a divisor of 5 would divide the left-hand side of (12), contrary to the fact that/? is distinct from q, Pi,--,pm. Next, suppose that q\(a-2k -B) or that q\(a + 2k -B). Equation (12) clearly implies in such a case, a = B = l (mod /?). Also if q\a-2k°B^ we must hav ...
On Sternâ•Žs Diatomic Sequence 0,1,1,2,1,3,2,3,1,4
... Stern’s diatomic sequence is a simply defined sequence with an amazing set of properties. Our goal is to present many of these properties—those that have most impressed the author. The diatomic sequence has a long history; perhaps first appearing in print in 1858 [28], it has been the subject of sev ...
... Stern’s diatomic sequence is a simply defined sequence with an amazing set of properties. Our goal is to present many of these properties—those that have most impressed the author. The diatomic sequence has a long history; perhaps first appearing in print in 1858 [28], it has been the subject of sev ...
Full text
... as a sum of non-consecutive Fibonacci numbers Fn , with initial terms F1 = 1, F2 = 2. We consider the distribution of the number of summands involved in such decompositions. Previous work proved that as n → ∞ the distribution of the number of summands in the Zeckendorf decompositions of m ∈ [Fn , Fn ...
... as a sum of non-consecutive Fibonacci numbers Fn , with initial terms F1 = 1, F2 = 2. We consider the distribution of the number of summands involved in such decompositions. Previous work proved that as n → ∞ the distribution of the number of summands in the Zeckendorf decompositions of m ∈ [Fn , Fn ...
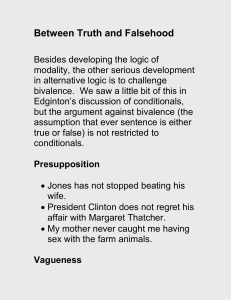
Between Truth and Falsity
... formulas will have 3n lines. It’s worth doing, maybe one. Exercise: Use a truth table to show that (p v q) ↔ (p →q) is not a tautology, but that the formulas are both weakly ...
... formulas will have 3n lines. It’s worth doing, maybe one. Exercise: Use a truth table to show that (p v q) ↔ (p →q) is not a tautology, but that the formulas are both weakly ...
Lesson 10: Writing and Expanding Multiplication Expressions
... numbers in a term together is called the coefficient of the term. After the word “term” is defined, students can be shown what it means to “collect like terms” using the distributive property. Expressions in expanded form are analogous to polynomial expressions that are written as a sum of monomi ...
... numbers in a term together is called the coefficient of the term. After the word “term” is defined, students can be shown what it means to “collect like terms” using the distributive property. Expressions in expanded form are analogous to polynomial expressions that are written as a sum of monomi ...
Numeracy - Parent Workshop
... I can round decimals to the nearest decimal place. I can recognise and use number patterns and relationships, I can reduce a fraction to its simplest form. I can order fractions and decimals. I understand simple ratio. I can find a simple fraction or percentage of a number or amount. I can + and – n ...
... I can round decimals to the nearest decimal place. I can recognise and use number patterns and relationships, I can reduce a fraction to its simplest form. I can order fractions and decimals. I understand simple ratio. I can find a simple fraction or percentage of a number or amount. I can + and – n ...