General Proof Theory - Matematički institut SANU
... Mac Lane wrote a doctoral thesis in proof theory under the supervision of Paul Bernays. In that thesis, contrary to the spirit of the proof theory that came to dominate the twentieth century, and in accordance with the spirit of general proof theory, he concentrated on the justification of the infere ...
... Mac Lane wrote a doctoral thesis in proof theory under the supervision of Paul Bernays. In that thesis, contrary to the spirit of the proof theory that came to dominate the twentieth century, and in accordance with the spirit of general proof theory, he concentrated on the justification of the infere ...
MAT 140 Discrete Mathematics I
... which contains n units of a quantity, then you have m x n units of the quantity. In a certain sense, times always means the same as “of.” m groups of n each gives a total of m x n units. Why does “A times B” mean “A of B”? Then use distributive law and add if appropriate. From class: “Each fraction ...
... which contains n units of a quantity, then you have m x n units of the quantity. In a certain sense, times always means the same as “of.” m groups of n each gives a total of m x n units. Why does “A times B” mean “A of B”? Then use distributive law and add if appropriate. From class: “Each fraction ...
Mathematicians
... 'Witch of Agnesi' Is a curve misnamed by John Colson. John name the curve when he mistook the word (versiera) 'curve' for a similar word which means 'witch'. The equation for this bell-shaped curve was given the name 'witch of Agnesi' and it stuck and can be found in some textbooks today. 1738 she p ...
... 'Witch of Agnesi' Is a curve misnamed by John Colson. John name the curve when he mistook the word (versiera) 'curve' for a similar word which means 'witch'. The equation for this bell-shaped curve was given the name 'witch of Agnesi' and it stuck and can be found in some textbooks today. 1738 she p ...
PDF
... 1. Continue defining and exploring first-order theory of simple arithmetic, iQ. i Q is a first-order finite axiomatization of a “number-like” domain. Even though i Q is extremely weak as you see from Problem Set 3 from Boolos & Jeffrey, we can, nevertheless, show in constructive type theory, either ...
... 1. Continue defining and exploring first-order theory of simple arithmetic, iQ. i Q is a first-order finite axiomatization of a “number-like” domain. Even though i Q is extremely weak as you see from Problem Set 3 from Boolos & Jeffrey, we can, nevertheless, show in constructive type theory, either ...
Special Facts to Know
... Let s(n) be the sum of all the proper factors of n. Deficient – s(n) < n Perfect – s(n) = n Abundant – s(n) > n Let d(n) be the total number of digits in the prime factorization of n. Frugal / Economical – d(n) < n Equidigital – d(n) = n Extravagant / Wasteful – d(n) > n Let b(n) be the number of 1s ...
... Let s(n) be the sum of all the proper factors of n. Deficient – s(n) < n Perfect – s(n) = n Abundant – s(n) > n Let d(n) be the total number of digits in the prime factorization of n. Frugal / Economical – d(n) < n Equidigital – d(n) = n Extravagant / Wasteful – d(n) > n Let b(n) be the number of 1s ...
Notes
... SL or construct. We need to use a weaker form of or defined by Gödel and Kolmogorov. They use ∼∼ (α | ∼ α) for α | ∼ α where ∼ α is defined to be α → void. ...
... SL or construct. We need to use a weaker form of or defined by Gödel and Kolmogorov. They use ∼∼ (α | ∼ α) for α | ∼ α where ∼ α is defined to be α → void. ...
Course discipline/number/title: MATH 1050: Foundations of
... 7. Convert Hindu-Arabic numbers to their equivalents in Egyptian, Mayan, and Roman numeration systems. 8. Use multi-base blocks to convert numbers between base ten and other bases. 9. Apply set theory and Venn diagrams to solve problems. 10. Demonstrate an understanding of the properties of addition ...
... 7. Convert Hindu-Arabic numbers to their equivalents in Egyptian, Mayan, and Roman numeration systems. 8. Use multi-base blocks to convert numbers between base ten and other bases. 9. Apply set theory and Venn diagrams to solve problems. 10. Demonstrate an understanding of the properties of addition ...
Course Syllabus Credit Hours and Contact Hours Department:
... Course Name: Mathematics For Elementary School Teachers I Credit Hours and Contact Hours: ...
... Course Name: Mathematics For Elementary School Teachers I Credit Hours and Contact Hours: ...
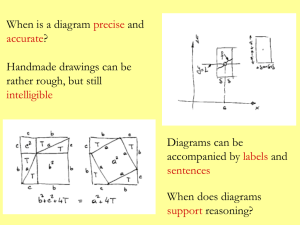
Diagrams in logic and mathematics - CFCUL
... Barwise - Etchemendy (1996), ‘Visual Information and Valid Reasoning’, in Allwein Barwise (eds.) (1996), Logical Reasoning with Diagrams, 3-25. Brown (1999), Philosophy of Mathematics: an introduction to the world of proofs and pictures. Giaquinto (2007), Visual Thinking in Mathematics. Polya (1945) ...
... Barwise - Etchemendy (1996), ‘Visual Information and Valid Reasoning’, in Allwein Barwise (eds.) (1996), Logical Reasoning with Diagrams, 3-25. Brown (1999), Philosophy of Mathematics: an introduction to the world of proofs and pictures. Giaquinto (2007), Visual Thinking in Mathematics. Polya (1945) ...