Maths Work Shop Presentation
... • It is most important for parents to talk and listen to children about their work in mathematics. • A lot of mathematics can be done using everyday situations and does not have to mean pencil and paper, e.g. when shopping, in the car or cooking. • You can really make a difference to your child by ...
... • It is most important for parents to talk and listen to children about their work in mathematics. • A lot of mathematics can be done using everyday situations and does not have to mean pencil and paper, e.g. when shopping, in the car or cooking. • You can really make a difference to your child by ...
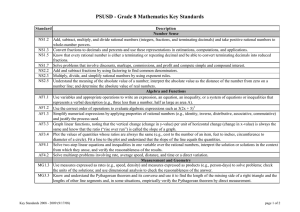
8th Grade Math CCSS Key Standards
... represents a verbal description (e.g., three less than a number, half as large as area A). ...
... represents a verbal description (e.g., three less than a number, half as large as area A). ...
Full text
... Cn is odd if and only if n = 2r - 1 for some positive integer v. Proof: The proof is based mainly on the following observation: If X is a finite set and a is an involution on X with fixed point set Xas then |z| = | j a | (mod 2); i.e.s \x\ and | j a | have the same parity,, Now let Dn denote the set ...
... Cn is odd if and only if n = 2r - 1 for some positive integer v. Proof: The proof is based mainly on the following observation: If X is a finite set and a is an involution on X with fixed point set Xas then |z| = | j a | (mod 2); i.e.s \x\ and | j a | have the same parity,, Now let Dn denote the set ...
verseny11 "In nature there cannot be two or more substances with
... if no two numbers were the same, then I have rolled seven distinct numbers. However, there are only six possible numbers I can roll with a die, so at least two numbers must have "collapsed" into one, that is, two were equal. This type of argument if called the pigeonhole principle (referring that se ...
... if no two numbers were the same, then I have rolled seven distinct numbers. However, there are only six possible numbers I can roll with a die, so at least two numbers must have "collapsed" into one, that is, two were equal. This type of argument if called the pigeonhole principle (referring that se ...