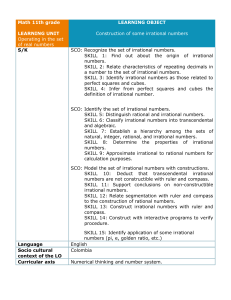
Bridge of Don Academy – Faculty of Mathematics Advanced Higher
... Notice that when we use the quadratic formula to solve an equation we will always get two roots: in the above example we obtain the roots z 2 i and z 2 i . In fact, for any equation with a complex root the conjugate of that complex number will also be a root. These roots provide us with fa ...
... Notice that when we use the quadratic formula to solve an equation we will always get two roots: in the above example we obtain the roots z 2 i and z 2 i . In fact, for any equation with a complex root the conjugate of that complex number will also be a root. These roots provide us with fa ...
Gentzen`s original consistency proof and the Bar Theorem
... the notion of a reduction procedure for deductions of sequents in the formal system of first-order number theory in natural deduction and an assignment of ordinals to these deductions such that each reduction step results in a decrease in ordinal. A reduction tree for a deduced sequent, along with a ...
... the notion of a reduction procedure for deductions of sequents in the formal system of first-order number theory in natural deduction and an assignment of ordinals to these deductions such that each reduction step results in a decrease in ordinal. A reduction tree for a deduced sequent, along with a ...
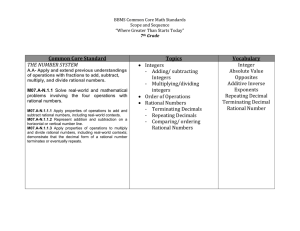
8•7 Lesson 1 Lesson Summary
... Perfect square numbers are those that are a product of an integer factor multiplied by itself. For example, the number 25 is a perfect square number because it is the product of 5 multiplied by 5. When the square of the length of an unknown side of a right triangle is not equal to a perfect square, ...
... Perfect square numbers are those that are a product of an integer factor multiplied by itself. For example, the number 25 is a perfect square number because it is the product of 5 multiplied by 5. When the square of the length of an unknown side of a right triangle is not equal to a perfect square, ...
Intuitionistic and Modal Logic
... Completeness of Predicate Logic • Let C0, C1, C2, · · · be a sequence of disjoint countably infinite sets of new constants. It suffices to consider theories in the languages Ln obtained by adding C0 ∪ C1 · · · ∪ Cn to the original language L. We consider theories containing ∃xϕ(x) → ϕ(cϕ) as in the ...
... Completeness of Predicate Logic • Let C0, C1, C2, · · · be a sequence of disjoint countably infinite sets of new constants. It suffices to consider theories in the languages Ln obtained by adding C0 ∪ C1 · · · ∪ Cn to the original language L. We consider theories containing ∃xϕ(x) → ϕ(cϕ) as in the ...







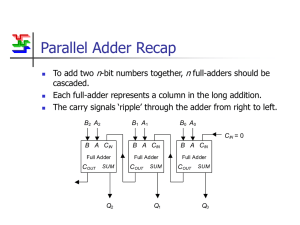
![arXiv:math/0412079v2 [math.NT] 2 Mar 2006](http://s1.studyres.com/store/data/013294887_1-d94fad656ee5fb5bde358f5c8c1d35cf-300x300.png)