Maxwell`s equations
... The potentials uniquely determine the fields, but the fields do not uniquely determine the potentials, e.g. arbitrary function of spacetime The field strength transforms as: result in the same electric and magnetic fields. More elegant relativistic notation: ...
... The potentials uniquely determine the fields, but the fields do not uniquely determine the potentials, e.g. arbitrary function of spacetime The field strength transforms as: result in the same electric and magnetic fields. More elegant relativistic notation: ...
Document
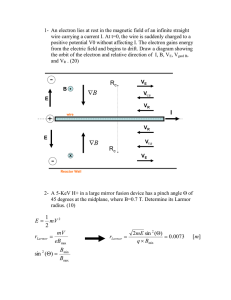
... each other. How strong is the magnetic induction B when E is equal to 10 V/m. (20) d qB E VE g is tan ce ...
... each other. How strong is the magnetic induction B when E is equal to 10 V/m. (20) d qB E VE g is tan ce ...
QM-01
... • Wave-particle duality- matter can behave both like particles as well as waves. Louis de Broglie • If a particle of mass m moves with a velocity v then it behaves like a matter wave having a wavelength λ given by, λ= ...
... • Wave-particle duality- matter can behave both like particles as well as waves. Louis de Broglie • If a particle of mass m moves with a velocity v then it behaves like a matter wave having a wavelength λ given by, λ= ...
Midterm Exam No. 02 (Spring 2014)
... 4. (20 points.) A charged particle with charge q moves on the z-axis with constant speed v, β = v/c. The electric and magnetic field generated by this charged particle is given by E(r, t) = (1 − β 2 ) ...
... 4. (20 points.) A charged particle with charge q moves on the z-axis with constant speed v, β = v/c. The electric and magnetic field generated by this charged particle is given by E(r, t) = (1 − β 2 ) ...
Syllabus PHYS 441
... A survey of concepts in particle and nuclear physics. We will learn about particles and forces that make up this universe, modern theories about these forces, culminating into an "almost theory of everything" known as the standard model of particle physics. We will learn about the Higgs boson and, t ...
... A survey of concepts in particle and nuclear physics. We will learn about particles and forces that make up this universe, modern theories about these forces, culminating into an "almost theory of everything" known as the standard model of particle physics. We will learn about the Higgs boson and, t ...
Chapter 7
... how light acts as both a particle and as a wave. Atomic Spectroscopy was developed to explore the ...
... how light acts as both a particle and as a wave. Atomic Spectroscopy was developed to explore the ...
Introduction to electromagnetism - Pierre
... Unification also serve as guiding principle for theory development, and ...
... Unification also serve as guiding principle for theory development, and ...
notes - UBC Physics
... its rest frame. Now consider what happens when we act on this state with rotation operators. Since the conserved quantity associated with rotations is angular momentum, the operators that give the change in the state if we make an infinitesimal rotation around the x, y, or z axes are the angular mom ...
... its rest frame. Now consider what happens when we act on this state with rotation operators. Since the conserved quantity associated with rotations is angular momentum, the operators that give the change in the state if we make an infinitesimal rotation around the x, y, or z axes are the angular mom ...
Wave-Particle Duality - the Principle of Complementarity The
... For a single electron, the wave function is the probability of finding the electron at that point. In the classical mechanics we use Newton’s equations of motion to describe particles positions and velocities, in the classical electrodynamics we use Maxwell’s equations to describe the electric and m ...
... For a single electron, the wave function is the probability of finding the electron at that point. In the classical mechanics we use Newton’s equations of motion to describe particles positions and velocities, in the classical electrodynamics we use Maxwell’s equations to describe the electric and m ...
Dia 1
... Such an anomaly could jeopardize the renormalizability of massive vector theories. How can we assure that such anomalies stay harmless ? Should the small-distance behavior provide answers? This was an important reason for studying the scaling behavior of gauge theories. What is their small-distance ...
... Such an anomaly could jeopardize the renormalizability of massive vector theories. How can we assure that such anomalies stay harmless ? Should the small-distance behavior provide answers? This was an important reason for studying the scaling behavior of gauge theories. What is their small-distance ...