compactness slides
... Suppose Φ̄ was not fs; then there would be some finite subset Γ that was not fs. ...
... Suppose Φ̄ was not fs; then there would be some finite subset Γ that was not fs. ...
overhead 7/conditional proof [ov]
... 3. Assumptions inside the scope of other assumptions must be discharged in the reverse order in which they were made. Numerous uses of IP can be made within a single proof; in fact a use of IP can be made WITHIN another use (or within a use of CP). When a use of IP is made within another use, the sc ...
... 3. Assumptions inside the scope of other assumptions must be discharged in the reverse order in which they were made. Numerous uses of IP can be made within a single proof; in fact a use of IP can be made WITHIN another use (or within a use of CP). When a use of IP is made within another use, the sc ...
Chapter 2 Review Extra Practice
... For each of the statements, write the conditional form and then the converse of the conditional. If the converse is true, combine the statements as a biconditional. 12. Rectangles have four sides. ...
... For each of the statements, write the conditional form and then the converse of the conditional. If the converse is true, combine the statements as a biconditional. 12. Rectangles have four sides. ...
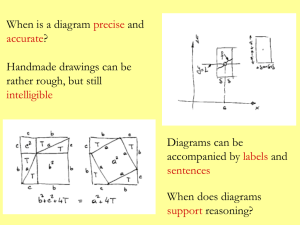
Diagrams in logic and mathematics - CFCUL
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
A Small Framework for Proof Checking - CEUR
... – If C is a direct function definition of form FUNC f: n := λx1 · · · xn t, then Γ2 is replaced by Γ2 { f := λx1 · · · xn t }. Direct predicate definitions are substituted away in the same way. – If C is an indirect function definition, it cannot be dropped, because we have no way of substituting it ...
... – If C is a direct function definition of form FUNC f: n := λx1 · · · xn t, then Γ2 is replaced by Γ2 { f := λx1 · · · xn t }. Direct predicate definitions are substituted away in the same way. – If C is an indirect function definition, it cannot be dropped, because we have no way of substituting it ...
7. Prime Numbers Part VI of PJE
... “Interesting” problems concerning primes. The following are conjectures and are all examples of problems that can be simply stated yet for which the answers are as yet unknown. 1) Goldbach’s Conjecture, Is every even integer n ≥ 4 the sum of two primes? ...
... “Interesting” problems concerning primes. The following are conjectures and are all examples of problems that can be simply stated yet for which the answers are as yet unknown. 1) Goldbach’s Conjecture, Is every even integer n ≥ 4 the sum of two primes? ...
solution
... Then m = s and {p1 , p2 , . . . , pm } = {q1 , q2 , . . . , qs }. That is, the sets of primes are equal but their elements are not necessarily listed in the same order; that is pi may or may not equal qi . Moreover, if pi = qj then ri = tj . In other words, if we express the same natural number as a ...
... Then m = s and {p1 , p2 , . . . , pm } = {q1 , q2 , . . . , qs }. That is, the sets of primes are equal but their elements are not necessarily listed in the same order; that is pi may or may not equal qi . Moreover, if pi = qj then ri = tj . In other words, if we express the same natural number as a ...
Chapter 3.6 Fundamental Theorem of Algebra
... You have learned several important properties about real roots of polynomial equations. ...
... You have learned several important properties about real roots of polynomial equations. ...
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems—and generally accepted statements, such as axioms. The proof of a mathematical theorem is a logical argument for the theorem statement given in accord with the rules of a deductive system. The proof of a theorem is often interpreted as justification of the truth of the theorem statement. In light of the requirement that theorems be proved, the concept of a theorem is fundamentally deductive, in contrast to the notion of a scientific theory, which is empirical.Many mathematical theorems are conditional statements. In this case, the proof deduces the conclusion from conditions called hypotheses or premises. In light of the interpretation of proof as justification of truth, the conclusion is often viewed as a necessary consequence of the hypotheses, namely, that the conclusion is true in case the hypotheses are true, without any further assumptions. However, the conditional could be interpreted differently in certain deductive systems, depending on the meanings assigned to the derivation rules and the conditional symbol.Although they can be written in a completely symbolic form, for example, within the propositional calculus, theorems are often expressed in a natural language such as English. The same is true of proofs, which are often expressed as logically organized and clearly worded informal arguments, intended to convince readers of the truth of the statement of the theorem beyond any doubt, and from which a formal symbolic proof can in principle be constructed. Such arguments are typically easier to check than purely symbolic ones—indeed, many mathematicians would express a preference for a proof that not only demonstrates the validity of a theorem, but also explains in some way why it is obviously true. In some cases, a picture alone may be sufficient to prove a theorem. Because theorems lie at the core of mathematics, they are also central to its aesthetics. Theorems are often described as being ""trivial"", or ""difficult"", or ""deep"", or even ""beautiful"". These subjective judgments vary not only from person to person, but also with time: for example, as a proof is simplified or better understood, a theorem that was once difficult may become trivial. On the other hand, a deep theorem may be simply stated, but its proof may involve surprising and subtle connections between disparate areas of mathematics. Fermat's Last Theorem is a particularly well-known example of such a theorem.





![overhead 7/conditional proof [ov]](http://s1.studyres.com/store/data/001382039_1-0b1da7da92f361d09e7b75df5e92d0f1-300x300.png)