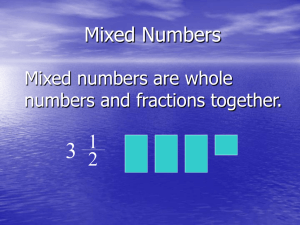Strategies for Multiplication Facts
... the facts for 4s,6s, 7s and 8s, other than Doubling or Counting Up or Down from a Known Fact, the Commutative Property of Multiplication will help children realize that they do not have as many facts to remember for these numbers as they think. ...
... the facts for 4s,6s, 7s and 8s, other than Doubling or Counting Up or Down from a Known Fact, the Commutative Property of Multiplication will help children realize that they do not have as many facts to remember for these numbers as they think. ...
Negative Numbers
... We will see later that we can do this in hardware with only one addition by making the carry in be 1. CS031 ...
... We will see later that we can do this in hardware with only one addition by making the carry in be 1. CS031 ...
Taxicabs and Sums of Two Cubes - Mathematics
... Are there numbers that can be written as a sum of two (positive) cubes in lots of different ways? The answer, as we shall see, involves a fascinating blend of geometry, algebra and number theory. And at the risk of prematurely revealing the punchline, the answer to our question is ...
... Are there numbers that can be written as a sum of two (positive) cubes in lots of different ways? The answer, as we shall see, involves a fascinating blend of geometry, algebra and number theory. And at the risk of prematurely revealing the punchline, the answer to our question is ...
Week 1: First Examples
... 4, which follows the prime number 3. Test this out with a few other square numbers, and you may begin to suspect, like I did, that a square number will rarely, if ever, come right after a prime number. What I am claiming, though, is that no square number aside from 4 will ever come immediately after ...
... 4, which follows the prime number 3. Test this out with a few other square numbers, and you may begin to suspect, like I did, that a square number will rarely, if ever, come right after a prime number. What I am claiming, though, is that no square number aside from 4 will ever come immediately after ...
TWO VERY SPECIAL PYTHAGOREAN TRIANGLES
... with their perimeters as Pentagonal Numbers. Special Pythagorean Triangles are generated by Gopalan and Janaki [3]. An attempt has been made to find out special Pythagorean triangles with their area as Triangular Number as well as Pentagonal numbers. ...
... with their perimeters as Pentagonal Numbers. Special Pythagorean Triangles are generated by Gopalan and Janaki [3]. An attempt has been made to find out special Pythagorean triangles with their area as Triangular Number as well as Pentagonal numbers. ...
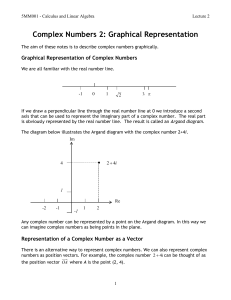
MM2009 Maths Methods 2
... We can also represent complex numbers as free vectors. The advantage of vector representation means that addition of complex numbers is then equivalent to the addition of the corresponding vectors. If z1 x1 y1i and z 2 x2 y2i then z1 z 2 x1 x2 y1 y2 i and z1 z 2 will form ...
... We can also represent complex numbers as free vectors. The advantage of vector representation means that addition of complex numbers is then equivalent to the addition of the corresponding vectors. If z1 x1 y1i and z 2 x2 y2i then z1 z 2 x1 x2 y1 y2 i and z1 z 2 will form ...
Modal logic and the approximation induction principle
... from the richest characterizations, which correspond to the canonical process equivalences, there are also finitary versions (denoted with a superscript ∗ ), which allow only conjunctions over a finite set. Intermediate equivalences based on formulas with arbitrary conjunctions but of finite depth a ...
... from the richest characterizations, which correspond to the canonical process equivalences, there are also finitary versions (denoted with a superscript ∗ ), which allow only conjunctions over a finite set. Intermediate equivalences based on formulas with arbitrary conjunctions but of finite depth a ...
Infinity

Infinity (symbol: ∞) is an abstract concept describing something without any limit and is relevant in a number of fields, predominantly mathematics and physics.In mathematics, ""infinity"" is often treated as if it were a number (i.e., it counts or measures things: ""an infinite number of terms"") but it is not the same sort of number as natural or real numbers. In number systems incorporating infinitesimals, the reciprocal of an infinitesimal is an infinite number, i.e., a number greater than any real number; see 1/∞.Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and early 20th centuries. In the theory he developed, there are infinite sets of different sizes (called cardinalities). For example, the set of integers is countably infinite, while the infinite set of real numbers is uncountable.